K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
2
3 tháng 9 2017
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân. b) Ta có AC // BE suy ra
= 
(3)
∆BDE cân tại B (câu a) nên 
= (4)
Từ (3) và (4) suy ra =
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (cmt - câu b)
=> Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
P/S : Mình lười vẽ hình nên chỉ mướn trên mạng nha!3 tháng 9 2017
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BÉ song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE \(\Rightarrow\widehat{C}_1=\widehat{E}\) (3)
∆BDE cân tại B (câu a) nên \(\Rightarrow\widehat{D_1}=\widehat{E}\) (4)
Từ (3) và (4) \(\Rightarrow\widehat{C_1}=\widehat{D_1}\)
Xét ∆ACD và ∆BCD có
AC = BD (gt)
\(\widehat{C_1}=\widehat{D_1}\) (cmt)
CD cạnh chung
\(\Rightarrow\) ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
\(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
G
1
HR
2 tháng 11 2016
a)\(\frac{3xy}{9y}=\frac{\left(3y\right)x}{3.\left(3y\right)}=\frac{x}{3}\)(đúng)
b)\(\frac{3xy+3}{9y+3}=\frac{3\left(xy+1\right)}{3\left(3y+1\right)}=\frac{xy+1}{3y+1}\ne\frac{x}{3}\)(sai)
c)\(\frac{3xy+3}{9y+9}=\frac{3\left(xy+1\right)}{9\left(y+1\right)}=\frac{xy+1}{3\left(y+1\right)}\ne\frac{x+1}{3+3}=\frac{x+1}{6}\)(sai)
d)\(\frac{3xy+3x}{9y+9}=\frac{3y\left(y+1\right)}{9\left(y+1\right)}=\frac{x}{3}\)(đúng)
TB
4
H
4
LM
18 tháng 1 2019
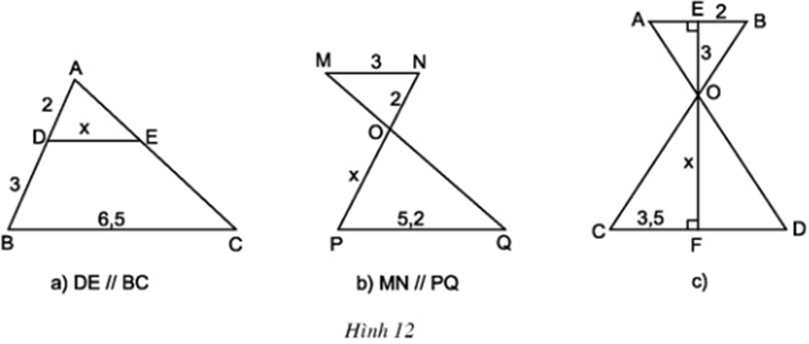
Lời giải
Áp dụng định lí Ta – lét ta có:
- Hình a:
- Hình b:
- Hình c:
18 tháng 1 2019
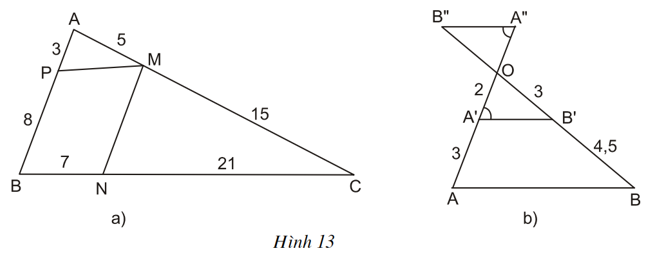
Bài 6 (trang 62 SGK Toán 8 tập 2): Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
Lời giải:
a) Xét hình 13a) : MN // AC.
⇒ MN // AB (Theo định lý Ta-let đảo).
b) Xét hình 13b) : AB // A’B’ // A”B”.
Ta có: 
⇒ A’B’ // A”B” (Hai góc so le trong bằng nhau).
Lại có:
Vậy ta có AB//A’B’//A”B”.
Kiến thức áp dụng
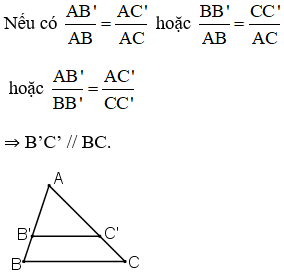
Định lý Ta-let đảo :
+ Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
ΔABC, B’ ∈ AB, C’ ∈ AC.
8 tháng 10 2019
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
8 tháng 10 2019
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
NK
1
7 tháng 10 2015
.
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
Suy ra EF // HG (1)
Tương tự EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = AC.
HG là đường trung bình của ∆ACD nên HG = AC.
Suy ra EF = HG
Lại có EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)
TB
1
31 tháng 8 2017
| ?1 |
a,
Hình a,
Xét tứ giác ABCD
Có: góc B = góc A2 = 60 độ
mà góc B và góc A2 là hai góc so le trong
=> BC // AD
=> tứ giác ABCD là hình thang
Hình b,
Xét tứ giác EFGH
Có: góc G + góc H = 105 độ + 75 độ = 180 độ
mà góc G và góc H là hai góc trong cùng phía
=>EH // FG
=> tứ giác EFGH là hình thang
Hình c,
Xét tứ giác INKM
Có góc I = 75 độ, góc N2 = 120 độ => góc I #( khác) góc N2
mà góc I và góc N2 là hai góc đồng vị
=> tứ giác INKM không là hình thang
b,
Xét hình a,
Có: góc A + góc A2 = 180 độ( hai góc kề bù)
góc A = 180 độ - góc A2
góc A = 180 độ - 60 độ
góc A = 120 độ
Cạnh bên là AB
Hai góc kề một cạnh bên AB là góc A và góc B
Có: góc A + góc B = 60 độ + 120 độ = 180 độ
=> Hai góc kề một cạnh bên của hình thang có tổng số đo bằng 180 độ hay hai góc kề một cạnh bên của hình thang bù nhau
Tương tự với hình b
| ?2 |
a,
Hình 16:
Nối A với C
Xét tam giác ADC và tam giác CBA
Có: + góc DCA = góc BAC ( do AB // CD mà đây là hai góc so le trong)
+ Cạnh AC chung
+ góc DAC = góc BCA ( do AD // BC mà đây là hai góc so le trong)
=> tam giác ADC = tam giác CBA ( g.c.g)
=> AD = BC ( hai cạnh tương ứng)
=> AB = CD ( hai cạnh tương ứng)
Hình 17:
Nối A với C
Xét tam giác ABC và tam giác CDA
Có: + AB = CD ( gt)
+ góc BAC = góc DCA( do AB // CD mà đây là hai góc so le trong)
+ cạnh AC chung
=> tam giác ABC = tam giác CDA ( c.g.c)
=> AD = BC ( hai cạnh tương ứng )
=> góc DAC = góc BCA ( hai góc tương ứng)
mà hai góc DAC và BCA là hai góc so le trong
--> AD //BC
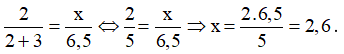
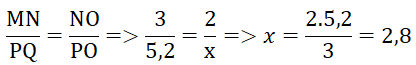
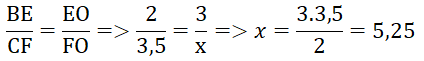
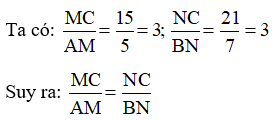
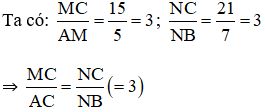
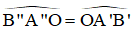
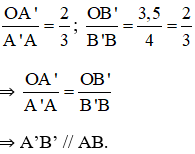
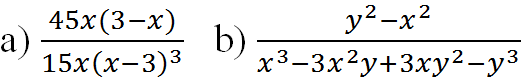
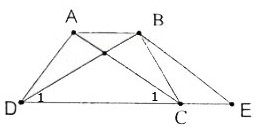
Bài giải: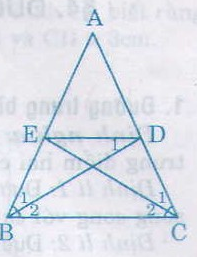
a) ∆ABD và ∆ACE có
AB = AC (gt)
\(\widehat{A}\) chung
\(\widehat{B_1}=\widehat{C_1}\left(=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}\widehat{C}\right)\)
Nên ∆ABD = ∆ACE (g.c.g)
Suy ra AD = AE
Chứng minh BEDC là hình thang cân như câu a của bài 15.
b) Vì BEDC là hình thang cân nên DE // BC.
Suy ra \(\widehat{D_1}=\widehat{B_2}\) (so le trong)
Lại có \(\widehat{B_2}=\widehat{B_1}\) nên \(\widehat{B_1}=\widehat{D_1}\)
Do đó tam giác EBD cân. Suy ra EB = ED.
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Chúc bạn học tốt!
bạn @Phạm Hoàng Giang ơi lời giải hay hả bạn ?