K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
![LỜI GIẢI] Cho tứ diện đều ABCD. Gọi varphi là góc giữa đường thẳng AB và mặt phẳng ( BCD ). Tính cos varphi - Tự Học 365](https://images.tuyensinh247.com/picture/2019/0301/1_7.jpg)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.
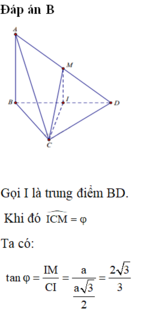
Gọi giao điểm của AP với BD là M
Xét ΔABD có
P là trọng tâm
M là giao điểm của AP với BD
Do đó: M là trung điểm của BD
Xét ΔDBC có
M,Q lần lượt là trung điểm của DB,DC
=>MQ là đường trung bình
=>MQ//BC
Chọn mp(AQM) có chứa PQ
Xét (AQM) và (ABC) có
\(A\in\left(AQM\right)\cap\left(ABC\right)\)
MQ//BC
Do đó: (AQM) giao (ABC)=xy, xy đi qua A và xy//MQ//BC
Gọi giao của PQ với xy là K
=>K là giao điểm của PQ với mp(ABC)