Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(A=\left(x^3.x^3.x^2\right).\left(y.y^4\right).\left(\frac{2}{5}.\frac{-5}{4}\right)\)
\(A=x^8.y^5.\left(-\frac{1}{2}\right)\)
\(B=\left(x^5.x.x^2\right).\left(y^4.y^2.y\right).\left(\frac{-3}{4}.\frac{-8}{9}\right)\)
\(B=x^8.y^7.\frac{2}{3}\)
Bài 2:
\(A=\left(15.x^2.y^3-12.x^2.y^3\right)+\left(11x^3.y^2-8.x^3.y^2\right)+\left(7x^2-12x^2\right)\)
\(A=3.x^2.y^3+2.x^3.y^2-5x^2\)
B tương tự nhé, đáp án là (theo mình)
\(B=\frac{5}{2}.x^5.y+\frac{7}{3}.x.y^4-\frac{1}{4}.x^2.y^3\)

a.
\(3x^2\left(2x^3-x+5\right)=6x^5-3x^3+15x^2\)
\(\Rightarrow6x^5-3x^3+15x^2=6x^5-3x^3+15x^2\)
\(=6x^5-3x^2+15x^2-6x^5-3x^3+15x^2\)
= 0
b.
\(\left(4xy+3y-5x\right)x^2y=4x^3y^2+3x^2y^2-5x^3y\)
\(\Rightarrow4x^3y^2+3x^2y^2-5x^3y=4x^3y^2+3x^2y^2-5x^3y\)
= 0

Lời giải:
Nếu $a\neq 0$ thì đa thức $M$ có bậc là $12+3=15\neq 5$ (trái với đề bài)
Nếu $a=0$ thì $M=-2xy+6x^3y^2$ có bậc $3+2=5$ (thỏa mãn)
Vậy $a=0$
---------------------
$N=-3xy^4+6x^3y^7+(a+1)x^3y^7-7xy$
$=-3xy^4+(a+7)x^3y^7-7xy$
Nếu $a+7\neq 0$ thì bậc của $N$ là $3+7=10\neq 5$ (trái đề)
Nếu $a+7=0$ thì $N=-3xy^4-7xy$ có bậc $1+4=5$ (thỏa đề)
Vậy $a+7=0\Leftrightarrow a=-7$

1: \(=3x^4+3x^2y^2+2x^2y^2+2y^4+2y^2\)
\(=\left(x^2+y^2\right)\left(3x^2+2y^2\right)+2y^2\)
\(=3x^2+2y^2+2y^2=3x^2+4y^2\)
2: \(=7\left(x-y\right)+4a\left(x-y\right)-5\)
=-5
3: \(=\left(x-y\right)\left(x^2+xy+y^2\right)-xy\left(x-y\right)+3=3\)
4: \(=\left(x+y\right)^2-4\left(x+y\right)+1=9-12+1=-2\)

1) \(A=2xy^2+3xy-xy^2+5xy^2+5xy+1\)
a, \(A=2xy^2+3xy-xy^2+5xy^2+5xy+1\)
= \(6xy^2+8xy+1\)
b, giá trị của biểu thức tại x = 1 và y = 2 là:
\(A=6.1.2^2+8.1.2+1=41\)
2) và 3) bạ vt khó hiểu wa
2) đề bài này là tìm b.a.c á bn, ghi đề chưa rõ lắm nên tui cx pó tay
3)
a/ Có: \(4x+9=0\)
\(\Leftrightarrow4x=-9\Rightarrow x=-\dfrac{9}{4}\)
vậy.............
b/ Có: \(-5x+6=0\)
\(\Leftrightarrow-5x=-6\Rightarrow x=\dfrac{6}{5}\)
Vậy....................
c/ có: \(x^2-4=0\)
\(\Leftrightarrow x^2=4\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Vậy ..................
d/ Có: \(9-x^2=0\)
\(\Leftrightarrow x^2=9\Rightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
Vậy.............
e/ Có: \(\left(y+2\right)\left(3-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y+2=0\\3-y=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=-2\\y=3\end{matrix}\right.\)
Vậy...............
p/s: bài 3 này thuộc dạng cơ bản nên lần sau nhớ suy nghĩ trc khi đăng câu hỏi

e, \(x^7-80x^6+80x^5-80x^4+80x^3-80x^2+80x+15\)
đặt 80=x+1 ta đc
\(x^7-\left(x+1\right)x^6+\left(x+1\right)x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x+1\right)x+15=x^7-x^7-x^6+x^6+x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x+15=x+15=79+15=94\)

Câu 1: ĐẶt \(\frac{x}{5}=\frac{y}{4}=k\)\(\Rightarrow x=5k;......y=4k\)
Ta có: \(x^2y=\left(5k\right)^2.\left(4k\right)=400k^3=100\)
\(\Rightarrow k^3=\frac{1}{4}\Rightarrow k=\sqrt[3]{\frac{1}{4}}\)
Vậy \(x=5k=4\sqrt[3]{\frac{1}{4}}\)
\(y=4.\sqrt[3]{\frac{1}{4}}\)
Câu 3 4 5 tương tư:
câu 2. bạn biến đổi: \(5x=2y\Leftrightarrow\frac{x}{2}=\frac{y}{5}\)thì sẽ trở thành dạng quen thuộc ở trên. :))
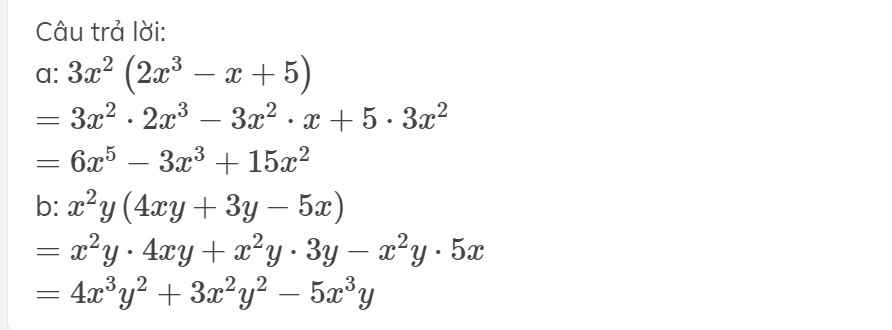
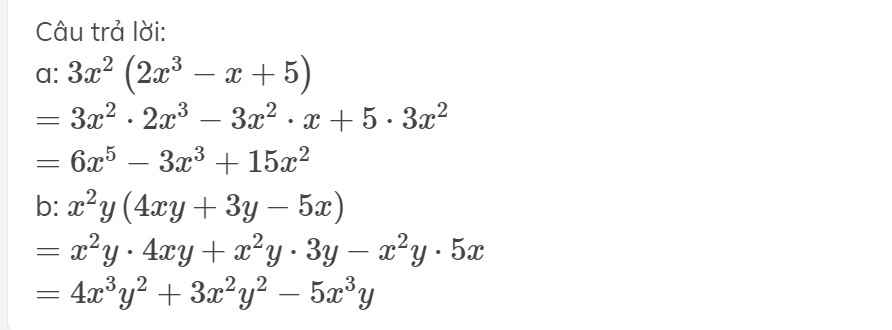
hangbich ơi chị nhớ em không????
luonghong567 ở trong hoidap247.com ý