Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
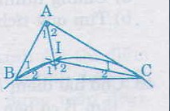
Theo tính chất của góc ngoài tam giác, ta có;
\(\widehat{I_2}=\widehat{A_1}+\widehat{B_1}\) (1)
\(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\) (2)
Cộng vế (1) và (2) vế với vế:
\(\widehat{I_1}+\widehat{I_2}=\widehat{A_1}+\widehat{A_2}+\widehat{B_1}+\widehat{C_1}\)
Hay \(\widehat{I}=90^o+45^o=135^o\)
Điểm I nhìn đoạn thẳng BC cố định dưới góc 135o không đổi, vậy quỹ tích của I là góc cung chứa góc 135o dựng trên đoạn thẳng BC
Một CTV gương mẫu chưa từng thấy! :)
Vậy mà cũng là CTV học tập! :)
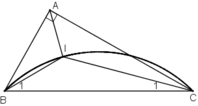
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135 º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135 º dựng trên đoạn BC.
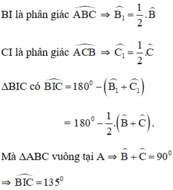
⇒ I thuộc cung chứa góc 135 º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135 º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135 º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của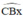 
+ Kẻ tia Cy sao cho CI là phân giác của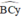 
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
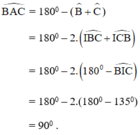
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135 º dựng trên đoạn BC (khác B và C).
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước :
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích : gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm M thỏa mãn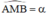 
(với A, B cố định, α không đổi) là cung chứa góc α dựng trên đoạn AB. (Cách dựng xem SGK).
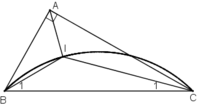
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135º dựng trên đoạn BC.
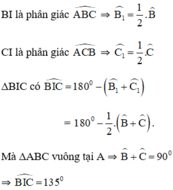
⇒ I thuộc cung chứa góc 135º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của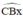 
+ Kẻ tia Cy sao cho CI là phân giác của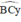 
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
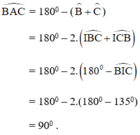
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135º dựng trên đoạn BC (khác B và C).
~ ~ ~ ~ ~
Tam giác HAB có HD là đường cao
\(\Rightarrow AH^2=AD\times AB\left(htl\right)\left(1\right)\)
Tam giác HAC có HE là đường cao
\(\Rightarrow AH^2=AE\times AC\left(htl\right)\left(2\right)\)
(1) và (2) => đpcm
~ ~ ~ ~ ~
HDA = DAE = AEH = 900
=> ADHE là hcn
=> EDH = AHD và HED = EHA
- - -
Tam giác DBH vuông tại D có DM là trung tuyến (M là trung điểm của BH)
=> DM = MH
=> Tam giác MDH cân tại M
=> MDH = MHD
Ta có: MDE = MDH + HDE = MHD + DHA = AHB = 900
=> MD _I_ DE
=> DE là tiếp tuyến của đường tròn (M ; MD) (3)
- - -
Tam giác ECH vuông tại E có EN là trung tuyến (N là trung điểm của CH)
=> EN = NH
=> Tam giác NEH cân tại N
=> NEH = NHE
Ta có: NED = NEH + HED = NHE + EHA = AHC = 900
=> NE _I_ DE
=> DE là tiếp tuyến của đường tròn (N ; NE) (4)
(3) và (4) => đpcm
~ ~ ~ ~ ~
Tam giác ABC vuông tại A có AH là đường cao:
(+) BC2 = AB2 + AC2 (ptg)
=> BC = 10 (cm)
(+) AB2 = BH . BC (htl)
=> BH = 3,6 (cm)
(+) AC2 = HC . BC (htl)
=> HC = 6,4 (cm)
\(DM=\dfrac{BH}{2}=1,8\left(cm\right)\)
\(EN=\dfrac{HC}{2}=3,2\left(cm\right)\)
MD _I_ DE và NE _I_ ED
=> MD // NE
=> MDEN là hình thang
Q là trung điểm của DE (ADHE là hcn)
P là trung điểm của MN (gt)
=> PQ là đtb của hình thang MDEN
\(\Rightarrow PQ=\dfrac{\left(DM+EN\right)}{2}=2,5\left(cm\right)\)
~ ~ ~ ~ ~
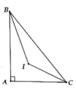
Tương tự câu 1
Tính được B I C ^ = 135 0
=> Quỹ tích của điểm I là hai cung chứa góc 135 0 dựng trên đoạn BC
Dùng BĐT Bunhiacopski:
Ta có: \(ac+bd\le\sqrt{a^2+b^2}.\sqrt{c^2+d^2}\)
Mà \(\left(a+c\right)^2+\left(b+d\right)^2\)
\(=a^2+b^2+2\left(ac+bd\right)+c^2+d^2\)
\(\le\left(a^2+b^2\right)+2\sqrt{a^2+b^2}.\sqrt{c^2+d^2}+c^2+d^2\)
\(\Rightarrow\sqrt{\left(a+c\right)^2+\left(b+d\right)^2}\le\sqrt{a^2+b^2}+\sqrt{c^2+d^2}\) (Đpcm)
Câu hỏi của Hoàng Khánh Linh - Toán lớp 8 - Học toán với OnlineMath copy nhớ ghi nguồn
cai nay thi cu chon dai mot gia tri ma ve thoi , day la dang tong quat cua do thi ham so noi thang ra no la duong thag
quỹ tích là ác mộng của mình đấy
tính góc BIC=....
do góc BIC không đổi=... mà cạnh BC cố định
=> I thuộc cung chứa góc....odựng trên BC cố định(ngoài 2 điểm B và C)
phần đảo: lấy I' thuộc cung vừa dựng .dễ dàng cm được góc BIC=BI'C(2 góc nội tiếp cùng chắn 1 cung) không đổi
kl:...quĩ tích điểm I...
p/s:toán quĩ tích cần xác định được điều cố định và không cố định .Nếu làm nhiều sẽ quen