Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D E K H 12 7,2 9 15
Bài làm
a) Xét tam giác DEK
Ta có: 152 = 225
92 + 122 = 225
=> 152 = 92 + 122 ( 225 = 225 )
Do đó: Tam giác DEK vuông tại D.
b) * Xét tam giác KDH vuông tại H
Theo định lý Pytago:
Ta có: DH2 = DK2 - HK2
hay DH2 = 122 - 7,22
=> DH2 = 144 - 51,84
=> DH2 = 92,16
=> DH = 9,6 ( cm )
* Chu vi của tam giác DHK là:
12 + 7,2 + 9,6 = 28,8 ( cm )
Vậy DH = 9,6 cm
Chu vi tam giác DHK: 28,8 cm
# Chúc bạn học tốt #

Lời giải:
a)
Ta thấy:
$9^2+12^2=15^2\Leftrightarrow EK^2+DK^2=DE^2$. Theo định lý Pitago đảo thì tam giác $DEK$ vuông tại $K$
b)
Áp dụng định lý Pitago đối với tam giác $DHK$ vuông có:
$DH=\sqrt{DK^2-KH^2}=\sqrt{12^2-7,2^2}=9,6$ (cm)
Chu vi tam giác $DHK$ là:$DK+DH+HK=12+9,6+7,2=28,8$ (cm)

A, Vì ABC cân tại A suy ra AB=AC; Góc B = góc C
Xét ABE và ACD có:
AB=AC cmt
BE=CD gt
Góc B = góc C cmt
=> ABE = ACD
B, Dễ thấy tam giác HBE = tam giác KCD (ch-gn)
=> EH=KD (đpcm) và BH=CK
C, vì BH=CK => AH=AK => tam giác AHK cân tại A => Góc AHK = 180-A/2 (1)
Vì tam giác ABC cân tại A => Góc B = 180-A/2 (2)
Từ 1 và 2 => Góc AHK = góc B mà ở vị trí đồng vị => HK // BC (đpcm)

a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
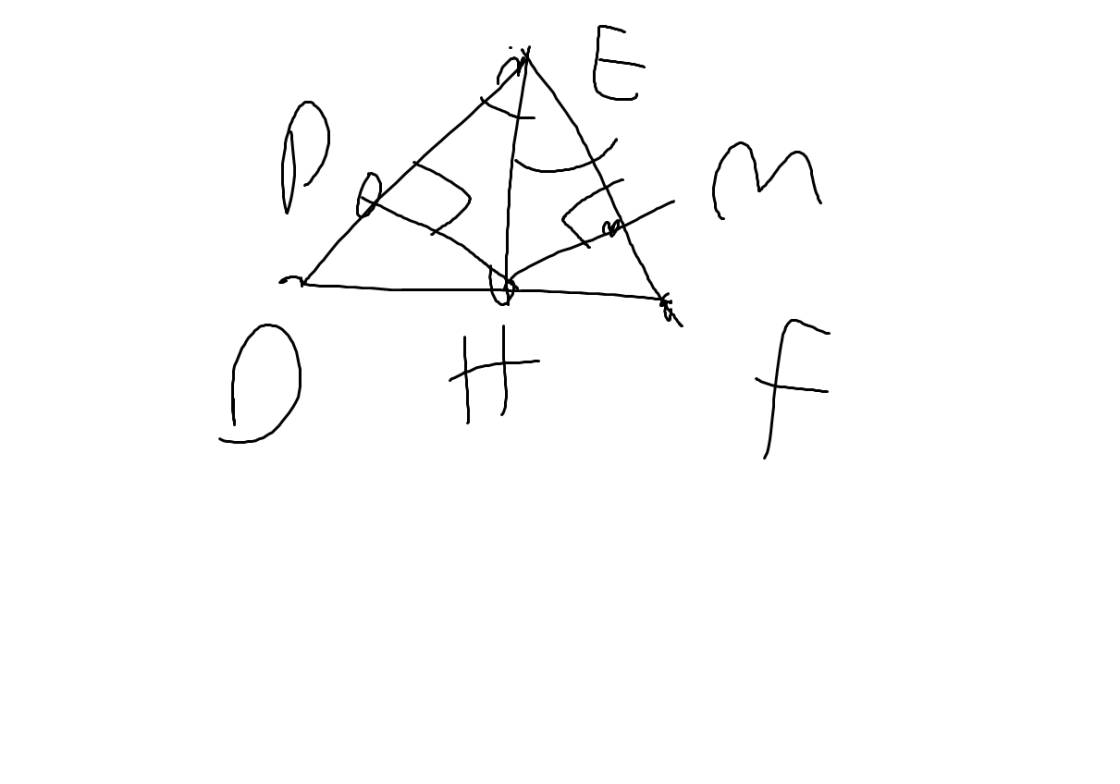

tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go

a: Xét ΔDEH vuông tại H và ΔKEH vuông tại H có
EH chung
ED=EK
DO đó: ΔDEH=ΔKEH
b: DK=18cm
nên DH=6cm
\(EH=\sqrt{12^2-6^2}=6\sqrt{3}\left(cm\right)\)
c: XétΔDEK có
H là trung điểm của DK
HM//DE
Do đó: M là trung điểm của EK
Ta có: ΔEHK vuông tại H
mà HM là đường trung tuyến
nên HM=KM