Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C 60 40 K
Xét \(\Delta ABC\) có \(\widehat{B}=40^o,\widehat{A}=60^o\)
\(\Rightarrow\widehat{BCA}=80^o\)
Mà : CK là tia phân giác của góc \(\widehat{BCA}\)
\(\Rightarrow\widehat{BCK}=\widehat{ACK}=\frac{80^o}{2}=40^o\)
Xét \(\Delta BKC\) có : \(\widehat{KBC}=\widehat{KCB}=40^o\)
\(\Rightarrow\Delta BKC\) cân ở K
\(\Rightarrow KB=KC\) (đpcm)

B A C K I D
a) Xét tam giác BAD và tam giác BHD có :
\(\widehat{BAD}=\widehat{BHD}=90^o\)
BD chung
\(\widehat{ABD}=\widehat{HBD}\) (Do BD là phân giác)
\(\Rightarrow\Delta BAD=\Delta BHD\) (Cạnh huyền góc nhọn)
\(\Rightarrow AB=HB\)
Ta cũng có \(\Delta BAD=\Delta BHD\) nên AD = HD.
Xét tam giác ADK và tam giác HDC có:
\(\widehat{KAD}=\widehat{CHD}=90^o\)
AD = HD
\(\widehat{ADK}=\widehat{HDC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta ADK=\Delta HDC\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow AK=HC\)
b) (Cô làm theo cách khi chưa học về các đường đồng quy trong tam giác)
Kéo dài BD cắt KC tại I.
Ta thấy BK = BA + AK = BH + HC = BC
Xét tam giác BKI và tam giác BCI có :
\(\widehat{KBI}=\widehat{CBI}\)
BI chung
BK = BC (CMT)
\(\Rightarrow\Delta BKI=\Delta BCI\) (c-g-c)
\(\Rightarrow\widehat{BIK}=\widehat{BIC}\) (Hai góc tương ứng)
Mà chúng lại là hai góc kề bù nên \(\widehat{BIK}=\widehat{BIC}=90^o\)
Vậy nên BD vuông góc KC.
c) Xét tam giác ABH có BA = BH nên nó là tam giác cân.
Vậy BD là phân giác thì đồng thời nó là đường cao.
Vậy BD vuông góc AH.
Lại có BD vuông góc KC nên AH // KC.
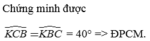
\(\widehat{ACB}=180^0-60^0-40^0=80^0\)
=>\(\widehat{KCB}=\dfrac{80^0}{2}=40^0\)
mà \(\widehat{KBC}=40^0\)
nên \(\widehat{KCB}=\widehat{KBC}\)
=>ΔKBC cân tại K
hay KB=KC