
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
Điều kiện: \(\left\{{}\begin{matrix}x\ne2\\y\ne0\end{matrix}\right.\)
HPT \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{\left|x-2\right|}+\dfrac{3}{y}=6\\\dfrac{6}{\left|x-2\right|}-\dfrac{2}{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{y}=5\\\dfrac{2}{\left|x-2\right|}=2-\dfrac{1}{y}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=1\\\left|x-2\right|=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\end{matrix}\right.\) (Thỏa mãn)
Vậy hệ phương trình có tập nghiệm \(\left(x;y\right)\in\left\{\left(4;1\right);\left(0;1\right)\right\}\)

8: \(x\sqrt{x}-1=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
9: \(x\sqrt{x}+1=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
10: \(x\sqrt{x}-y\sqrt{y}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\)
11: \(x\sqrt{x}+y\sqrt{y}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)

2:
a: \(A=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-6}{3}=-2\)
b: \(B=\dfrac{\left(x_1+x_2\right)^2-3x_1x_2}{1-x_1x_2}=\dfrac{36-3\cdot3}{1-3}=\dfrac{36-9}{-2}=-\dfrac{27}{2}\)
c: \(C=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-6\right)^2-4\cdot3}=2\sqrt{6}\)
d: \(D=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-3x_1x_2\)
\(=\left(-6\right)^3-3\cdot3\cdot\left(-6\right)-3\cdot3\)
=261

Đặt \(a=\sqrt[3]{9+4\sqrt{5}};b=\sqrt[3]{9-4\sqrt{5}}\Rightarrow A=a+b\)
Ta có : \(A^3=\left(a+b\right)^3=a^3+b^3+3ab\left(a+b\right)=a^3+b^3+3ab.A\)
\(=\left(9+4\sqrt{5}\right)+\left(9-4\sqrt{5}\right)+3\sqrt{\left(9-4\sqrt{5}\right)\left(9+4\sqrt{5}\right)}\)
\(\Rightarrow A=18+3A\Leftrightarrow A^3-3A-18\Leftrightarrow\left(A-3\right)\left(A^2+3A+6\right)\Rightarrow A=3\)

3:
ĐKXĐ: x>=0; x<>1
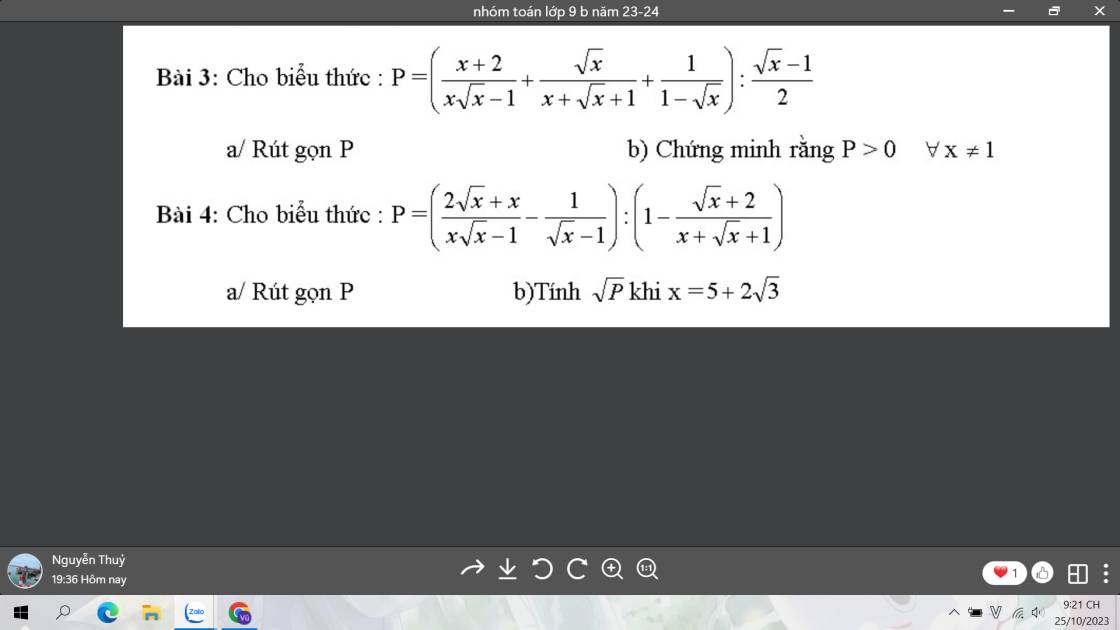
a: \(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0+1=1\)
=>\(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
mà 2>0
nên \(P=\dfrac{2}{x+\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ

3:
a: \(P=\dfrac{3x+3-2x+6\sqrt{x}-x-3\sqrt{x}}{x-9}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)
\(=\dfrac{3\sqrt{x}+3}{x-9}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{3}{\sqrt{x}+3}\)
b: Khi x=20-6căn 11 thì \(P=\dfrac{3}{\sqrt{11}-3+3}=\dfrac{3}{\sqrt{11}}\)
c: P>1/2
=>P-1/2>0
=>\(\dfrac{3}{\sqrt{x}+3}-\dfrac{1}{2}>0\)
=>6-căn x-3>0
=>3-căn x>0
=>0<x<9
 giải hộ em bài 3 và bài 4 nha
giải hộ em bài 3 và bài 4 nha 
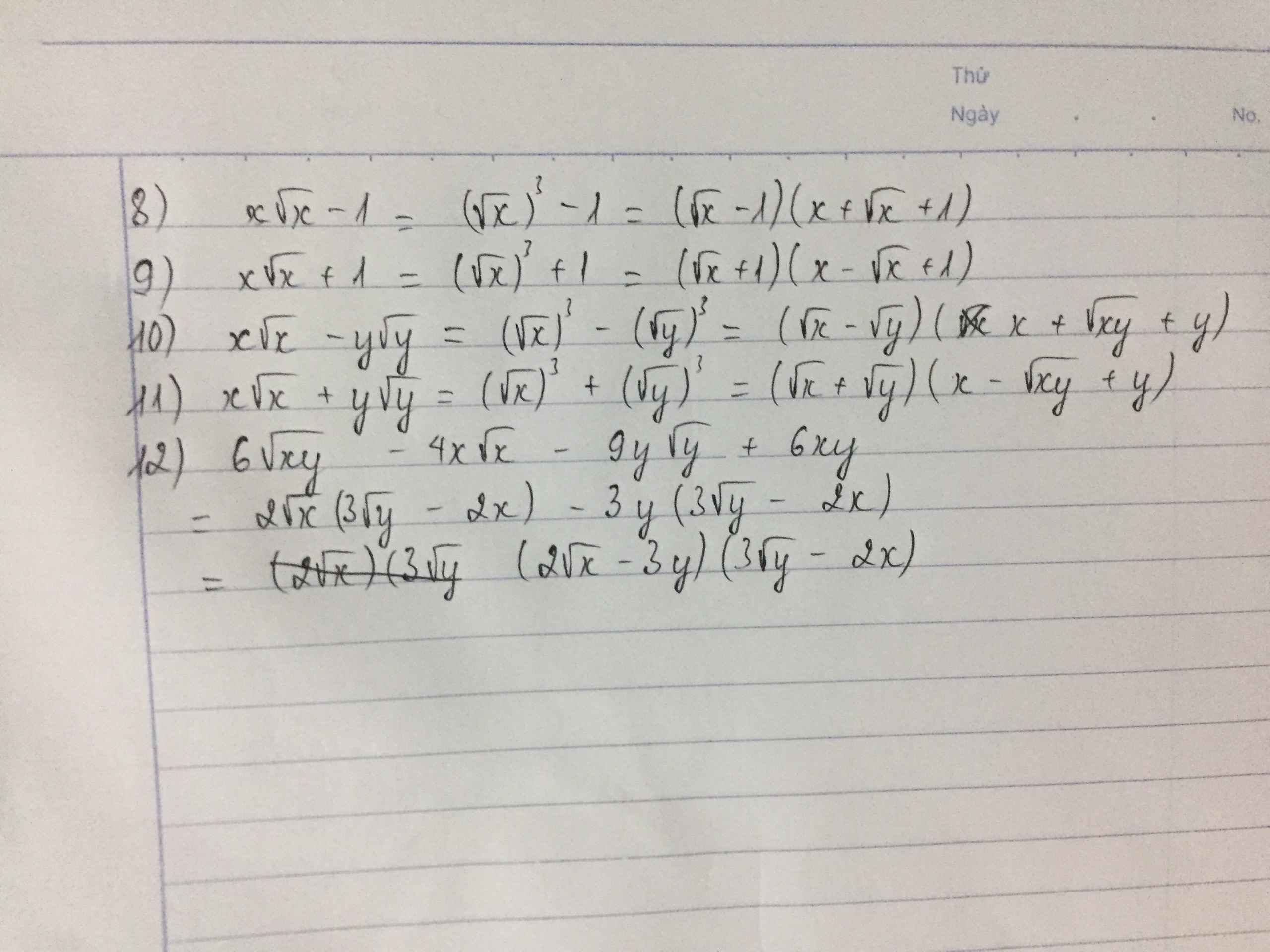

 giải giúp mik bài 3 nha mn <3
giải giúp mik bài 3 nha mn <3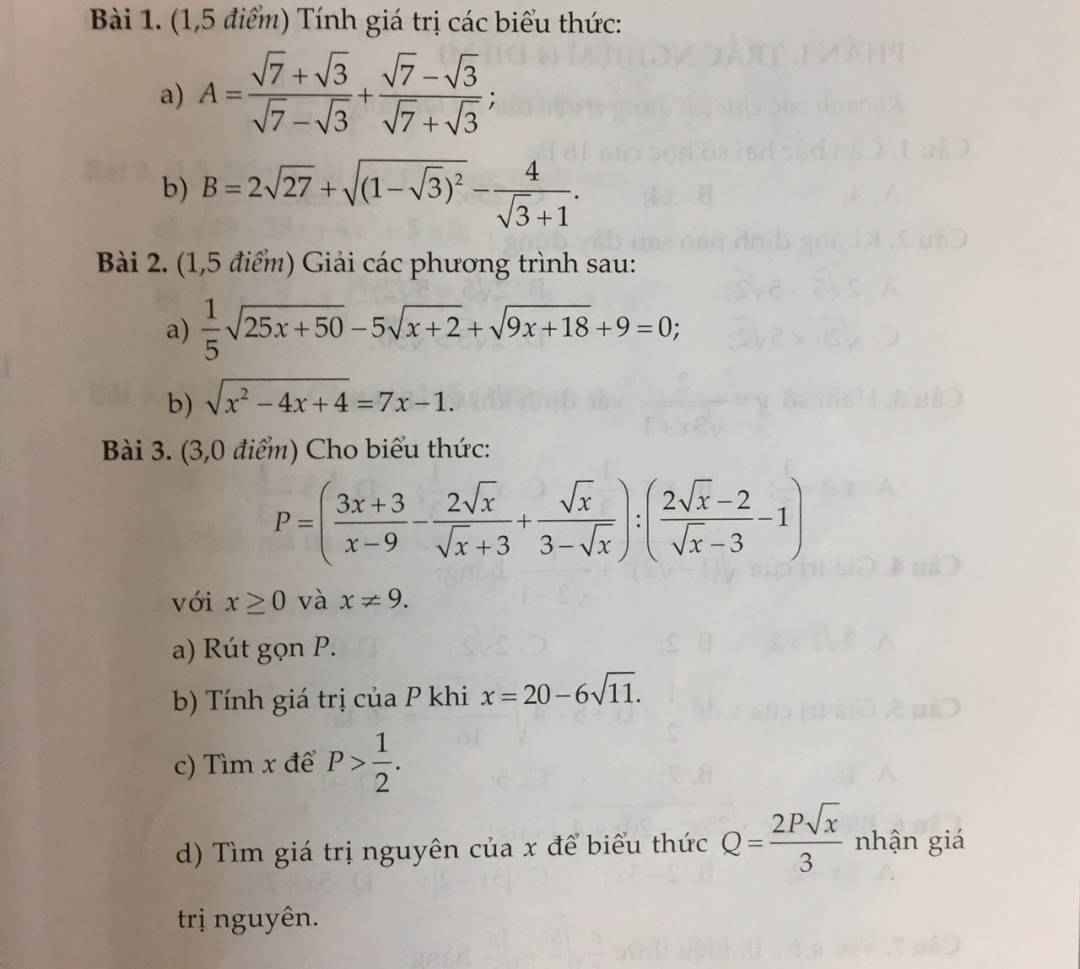 bài 3 nha giúp em
bài 3 nha giúp em
A B I K M D
Ta thấy \(\Delta KMB\sim\Delta MAB\left(g-g\right)\Rightarrow\frac{KM}{MA}=\frac{MB}{AB}=\frac{KB}{MB}\)
Vậy thì \(MB^2=AB.KB=\frac{AB^2}{4}\Rightarrow\frac{MB}{AB}=\frac{1}{2}\)
Suy ra \(\frac{KM}{MA}=\frac{1}{2}\)
Áp dụng Ta let ta có ngay \(PM=\frac{1}{3}AM=\frac{2}{3}KM=PI\)
Vậy PM = PI (đpcm)
Sao đề chỉ có dấu phẩy thế kia?