Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác BDCH có
BD//CH
BH//CD
Do đó: BDCH là hình bình hành

a) Vì BHCD có các cặp cạnh đối song song nên là hình bình hành.
b) Tứ giác ABCD có A B D ^ = A C D ^ = 90 0 m à B A C ^ = 60 0 nên B D C ^ = 120 0
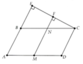

a)BH vuông góc với AC
CD vuông góc với AC =>BH//CD
Tương tự HC//BD =>BDCH là HBH
b)góc BDC=góc BHC
HC cắt AB tại E => góc AEH=900
HB cắt AC tại F => góc AFH=900
=>góc EHF=góc BHC= góc BDC
góc AEH+góc AFH+góc EHF+góc ABC =3600
=>góc BDC+góc ABC=1800

a)BH vuông góc với AC
CD vuông góc với AC =>BH//CD
Tương tự HC//BD =>BDCH là HBH
b)góc BDC=góc BHC
HC cắt AB tại E => góc AEH=900
HB cắt AC tại F => góc AFH=900
=>góc EHF=góc BHC= góc BDC
góc AEH+góc AFH+góc EHF+góc ABC =3600
=>góc BDC+góc ABC=1800

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

\(a,\) Vì H là trực tâm nên BH,CH là đường cao tam giác ABC
\(\Rightarrow BH\perp AC;CH\perp AB\\ \Rightarrow BH\text{//}CD;CH\text{//}BD\\ \Rightarrow BDCH\text{ là hbh}\)
\(b,BDCH\text{ là hbh}\Rightarrow\widehat{BHC}=\widehat{BDC}\\ \text{Xét tứ giác }ABCD:\widehat{BAC}+\widehat{BAD}+\widehat{DAC}+\widehat{BDC}=360^0\\ \Rightarrow\widehat{BAC}+\widehat{BDC}=360^0-90^0-90^0=180^0\\ \Rightarrow\widehat{BAC}+\widehat{BHC}=180^0\)
\(c,\) Gọi O là trung điểm AD \(\Rightarrow OA=OD=\dfrac{1}{2}AD\)
\(\Delta ABD\text{ và }\Delta ACD\text{ vuông tại }B,C\text{ có }BO,CO\text{ là trung tuyến ứng ch }AD\)
\(\Rightarrow BO=CO=\dfrac{1}{2}AD\)
Vậy \(AO=BO=CO=DO\) hay A,B,C,D cách đều O

a: Xét tứ giác BDCH có
BH//CD
BD//CH
Do đó: BDCH là hình bình hành
b: \(\widehat{BDC}=180^0-60^0=120^0\)
Xet tam giác ABC có H là trực tâm nên\(\hept{\begin{cases}CH\perp AB\\BH\perp AC\end{cases}}\)
Ta có \(\hept{\begin{cases}DB\perp AB\left(gt\right)\\CH\perp AB\left(cmt\right)\end{cases}\Rightarrow D}B//CH\)
\(\hept{\begin{cases}DC\perp AC\left(gt\right)\\BH\perp AC\left(cmt\right)\end{cases}\Rightarrow DC//BH}\)
Xét tứ giác BDCH có DB//CH (cmt) vầ DC//BH (cmt) nên tứ giác BDCH là hbh ( théo dấu hiệu nhận biết hbh) đpcm