Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cam là x, số quýt là y (x, y ∈ N* ; x < 17, y < 17).
Quýt, cam 17 quả tươi ⇒ x + y = 17.
Mỗi quả quýt chia ba ⇒ Có 3y miếng quýt
Chia mười mỗi quả cam ⇒ Có 10x miếng cam
Tổng số miếng tròn 100 ⇒ 10x + 3y = 100.
Ta có hệ phương trình:
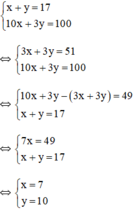
Vậy có 7 quả cam và 10 quả quýt.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.

Gọi số cam là x, số quýt là y (x, y ∈ N* ; x < 17, y < 17).
Quýt, cam 17 quả tươi ⇒ x + y = 17.
Mỗi quả quýt chia ba ⇒ Có 3y miếng quýt
Chia mười mỗi quả cam ⇒ Có 10x miếng cam
Tổng số miếng tròn 100 ⇒ 10x + 3y = 100.
Ta có hệ phương trình:
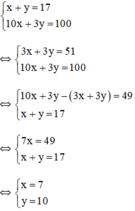
Vậy có 7 quả cam và 10 quả quýt.

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

Gọi số cam là x ( quả )
số quýt là y (quả)
Điều kiện x, y > 0
Theo đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=7\left(1\right)\\10x+3y=100\left(2\right)\end{matrix}\right.\)
(1) ⇔ y = 17 - x (3)
Thế (3) vào (2): 10x + 3(17 - x) = 100
⇔ 10x + 51 - 3x = 100 ⇔ 7x = 49 ⇔ x = 7
Từ đó y = 17 - 7 = 10
Vậy có 7 quả cam và 10 quả quýt.

Gọi số cam là x, số quýt là y. Điều kiện x, y là số nguyên dương.
Vậy có 7 quả cam và 10 quả quýt.
Gọi số quýt là x , số cam là y ( x ; y khác 0 )
Theo bài ra ta có :
\(x+y=17\)
\(\Rightarrow3\left(x+y\right)=51\left(1\right)\)
\(3x+10y=100\)
\(\Rightarrow3\left(x+y\right)+7y=100\left(2\right)\)
Lấy \(\left(2\right)-\left(1\right)\); ta được :
\(7y=100-51\)
\(\Rightarrow7y=49\)
\(\Rightarrow y=7\)
Mà \(x+y=17\)
\(\Rightarrow x=17-7=10\)
Vậy số quýt là 10 quả ; số cam là 7 quả

\(T=x^4+y^4+z^4\)
áp dụng bđt bunhia cốp -xki với bộ số \(\left(x^2,y^2,z^2\right);\left(1,1,1\right)\)
\(\left(\left[x^2\right]^2+\left[y^2\right]^2+\left[z^2\right]^2\right)\left(1^2+1^2+1^2\right)\ge\left(x^2+y^2+z^2\right)^2\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(2xy+2yz+2xz\right)^2}{3}\)(bđt tương đương)
\(\left(x^4+y^4+z^4\right)\ge\frac{4}{3}\)
dấu "=" xảy rakhi và chỉ khi
\(\hept{\begin{cases}\frac{x^2}{1}=\frac{y^2}{1}=\frac{z^2}{1}\\x=y=z=1\end{cases}< =>\frac{1^2}{1}=\frac{1^2}{1}=\frac{1^2}{1}}\)(luôn đúng)
vậy dấu "=" có xảy ra
\(< =>MIN:T=\frac{4}{3}\)
sửa dòng 3 dưới lên
\(T\ge\frac{\left(xy+yz+xz\right)^2}{3}=\frac{1}{3}\)
Dấu ''='' xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)
Vậy GTNN T là 1/3 khi \(x=y=z=\frac{\sqrt{3}}{3}\)

\(A=0.5\cdot4\sqrt{3-x}-\sqrt{3-x}-2\sqrt{3}+1=\sqrt{3-x}-2\sqrt{3}+1\) (xác định khi x=<3)
a)thay \(x=2\sqrt{2}\)vào a ra có
\(\sqrt{3-2\sqrt{2}}-2\sqrt{3}+1=\sqrt{\left(\sqrt{2}-1\right)^2}-2\sqrt{3}+1\)
\(=\sqrt{2}-1+2\sqrt{3}+1=\sqrt{2}+2\sqrt{3}\)
Để A=1<=> \(\sqrt{3-x}-2\sqrt{3}+1=1\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}+1-1=0\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}=0\\ \Leftrightarrow3-x=12\Leftrightarrow x=-9\)

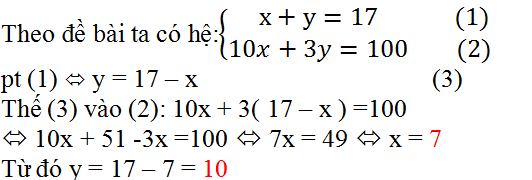
Bài 28
Đặt sô cần tìm là a và b (a>b)
ta có a+b=1006=> a=1006-b
a=b*2+124=> 1006-b= b*2 +124 => b= 294=> a= 712
bài 29
Gọi số cam là a
số quýt là b
ta có a+b=17=> a=17-b
3*b+a*10=100
=> 3*b+10*(17-b) = 100 => b=10=> a=7
Bài 28:
Gọi số lớn là x, số nhỏ là y (a, y ∈ N*); x > 124. Ta có: Tổng bằng 1006 nên được: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có điều kiện là y > 124 và có phương trình: x = 2y + 124
Ta có HPT:
\(\hept{\begin{cases}x+y=1006\\x=2y+124\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=1006\\x-2y=124\end{cases}}}\)
Vậy hai số tự nhiên phải tìm là 712 và 294.
Bài 29:
Gọi số cam là x, số quýt là y. Điều kiện x, y là số nguyên dương.
Theo đề bài, ta có HPT: \(\hept{\begin{cases}x+y=17\left(1\right)\\10x+3y=100\left(2\right)\end{cases}}\)
\(\text{PT}\left(1\right)\Leftrightarrow y=17-x\)
Thế (3) vào (2): 10x + 3(17 - x) = 100
<=> 10x + 51 - 3x = 100 <=> 7x = 49 <=> x = 7
=> y = 17 - 7 = 10
=> Có 7 quả cam và 10 quả quýt.