K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

LA
3 tháng 3 2018
a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm
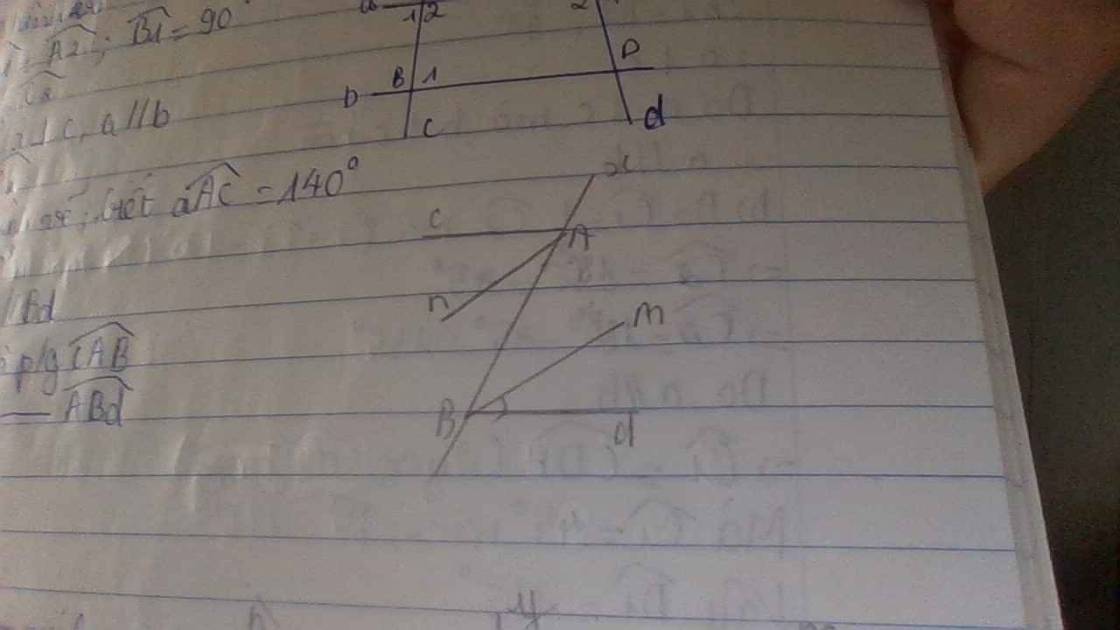
a) Để chứng minh rằng Ac//Bd, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn đều bằng 180 độ. Vì góc aAc = 140 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 140 độ + 40 độ = 180 độ. Do đó, ta có Ac//Bd.
b) Để chứng minh rằng Am là phân giác góc cABG, ta cần chứng minh rằng góc cAmB = góc cABG. Vì góc cAmB là góc nội tiếp trên cung cùng phía với góc cABG, nên góc cAmB = (180 độ - góc cABG) / 2 = (180 độ - 140 độ) / 2 = 40 độ. Vậy, Am là phân giác góc cABG.
c) Để chứng minh rằng An//Bm, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn là 180 độ. Vì góc cAmB = 40 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 40 độ + 40 độ = 80 độ. Do đó, ta không thể kết luận rằng An//Bm.
khó quaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaas