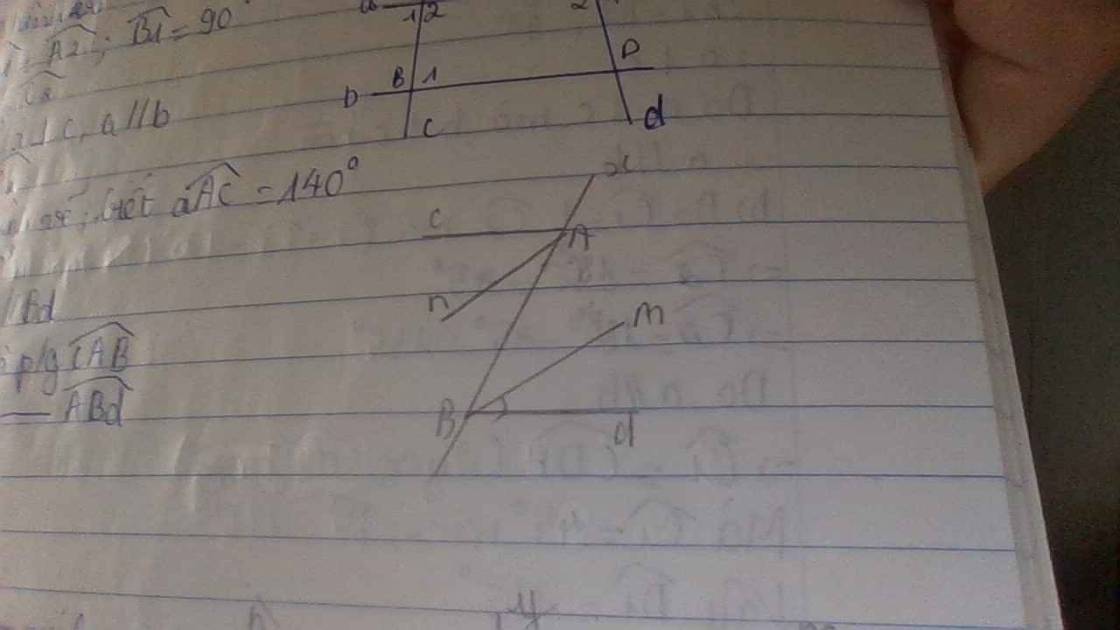Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để chứng minh rằng Ac//Bd, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn đều bằng 180 độ. Vì góc aAc = 140 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 140 độ + 40 độ = 180 độ. Do đó, ta có Ac//Bd.
b) Để chứng minh rằng Am là phân giác góc cABG, ta cần chứng minh rằng góc cAmB = góc cABG. Vì góc cAmB là góc nội tiếp trên cung cùng phía với góc cABG, nên góc cAmB = (180 độ - góc cABG) / 2 = (180 độ - 140 độ) / 2 = 40 độ. Vậy, Am là phân giác góc cABG.
c) Để chứng minh rằng An//Bm, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn là 180 độ. Vì góc cAmB = 40 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 40 độ + 40 độ = 80 độ. Do đó, ta không thể kết luận rằng An//Bm.

a)Vì BD//AM nên : Góc ABD=MAB(so le trong)
Góc DBC=AMC(đồng vị)
mà Góc ABD=DBC
Từ 3 điều này suy ra Góc MAB=AMC.
b)Gọi giao điểm của By với AM là H
tam giác BHM có : GÓc BHM=180-HMB+HBM
Tam giác ABH có: Góc BHA=180-BAH+ABH
mà BAH=BMH(cmt);HBM=HBA(gt)
Từ 3 điều này suy ra BHM=BHA
Lại có BHM+BHA=180 => BHM=BHA=\(\frac{180}{2}=90\)(độ).
Vậy By vuông góc với AM.
Vì câu này mình nhớ là học kì 1 bạn chưa học tới tính chất đường trung trực nên mới làm cách này, hoặc tính chất của tam giác cân. Nếu bạn học rồi thì sẽ ngắn hơn.
c)Theo định lí tổng 3 góc trong tam giác ta có:A+B+C=180
hay 60+B+50=180
B=180-110=70(độ)
=> ABD=CBD=\(\frac{70}{2}=35\)(độ
Theo định lí tổng 3 góc trong tam giác ta có: CBD+BDC+C=180
hay 35+BDC+50=180
BDC=180-85=95 độ.
a)Vì BD//AM nên : Góc ABD=MAB(so le trong)
Góc DBC=AMC(đồng vị)
mà Góc ABD=DBC
Từ 3 điều này suy ra Góc MAB=AMC.
b)Gọi giao điểm của By với AM là H
tam giác BHM có : GÓc BHM=180-HMB+HBM
Tam giác ABH có: Góc BHA=180-BAH+ABH
mà BAH=BMH(cmt);HBM=HBA(gt)
Từ 3 điều này suy ra BHM=BHA
Lại có BHM+BHA=180 => BHM=BHA=180/2 =90°
Vậy By vuông góc với AM.
Vì câu này mình nhớ là học kì 1 bạn chưa học tới tính chất đường trung trực nên mới làm cách này, hoặc tính chất của tam giác cân. Nếu bạn học rồi thì sẽ ngắn hơn.
c)Theo định lí tổng 3 góc trong tam giác ta có:A+B+C=180
hay 60+B+50=180
B=180-110=70°
=> ABD=CBD=70/2 =35°
Theo định lí tổng 3 góc trong tam giác ta có: CBD+BDC+C=180
hay 35+BDC+50=180
BDC=180-85=95°

Ta có hình vẽ:
A B C M N I 30 độ a/ Xét tam giác AIB và tam giác MIB có:
AB = MB (GT)
BI : cạnh chung
AI = IM (GT)
=> tam giác AIB = tam giác MIB (c.c.c)
b/ Ta có: tam giác AIB = tam giác MIB (câu a)
=> \(\widehat{BIA}\)=\(\widehat{BIM}\) (2 góc tương ứng)
Mà \(\widehat{BIA}\)+\(\widehat{BIM}\) = 1800 (kề bù)
=> \(\widehat{BIA}\)=\(\widehat{BIM}\)=900
=> BN\(\perp\)AM (đpcm)
c/ Trong tam giác ABC có:
\(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)=1800
hay 900 + \(\widehat{B}\) + 300 = 1800
=> \(\widehat{B}\)=600
Vì tam giác AIB = tam giác MIB (đã chứng minh trên câu a)
=> \(\widehat{ABI}\)=\(\widehat{MBI}\) (2 góc tương ứng)
Ta có: \(\widehat{ABI}\)=\(\widehat{MBI}\)=\(\frac{1}{2}\)\(\widehat{ABM}\)=\(\frac{1}{2}\)600 = 300
Trong tam giác BNC có:
\(\widehat{NBC}\)+\(\widehat{BCN}\)+\(\widehat{BNC}\) =1800
hay 300 + 300 + \(\widehat{BNC}\)=1800
=> \(\widehat{BNC}\) = 1200
Vậy \(\widehat{BNC}\)=1200 hay \(\widehat{INC}\)=1200