Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N H K
Kẻ MK//AB (\(K\in AH\)) \(\Rightarrow MK\perp AD\) , mà \(AH\perp DM\Rightarrow K\) là trực tâm tam giác \(AMD\Rightarrow DK\perp AM\)
Áp dụng Talet: \(\frac{HM}{BH}=\frac{MK}{AB}\)
Mà \(\frac{BM}{MH}=\frac{CN}{ND}\Leftrightarrow\frac{BM}{MH}+1=\frac{CN}{ND}+1\Leftrightarrow\frac{BH}{MH}=\frac{CD}{ND}\Leftrightarrow\frac{MH}{BH}=\frac{ND}{CD}\)
\(\Rightarrow\frac{MK}{AB}=\frac{ND}{CD}\Rightarrow MK=ND\) (do AB=CD)
Mà KM//AB//CD \(\Rightarrow MKDN\) là hbh (tứ giác có cặp cạnh đối song song và bằng nhau)
\(\Rightarrow DK//MN\Rightarrow MN\perp AM\Rightarrow\widehat{AMN}=90^0\)

a: Xét ΔHAB có
M là trung điểm của HA
N là trung điểm của HB
Do đó: MN là đường trung bình
=>MN//AB và MN=AB/2
=>MN//KC và MN=KC
=>NCKM là hình bình hành
b; Xét ΔBMC có
BH là đường cao
MN là đường cao
BH cắt MN tại N
DO đó:N là trực tâm
=>CN vuông góc với BM
=>BM vuông góc với MK
hay góc BMK=90 độ

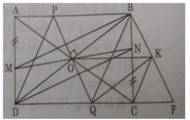
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.

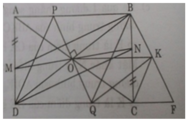
a) Ta có AD = BC; AD // BC (gt), AM = CN (gt)
⇒ AD – AM = BC – CN
Hay DM = BN
Lại có DM // BN
Do đó MNDN là hình bình hành ⇒ BM // DN