Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kết quả thống kê được ngày, tháng, năm sinh của các bạn trong lớp em như sau (được làm dưới hình thức là bảng tần số):
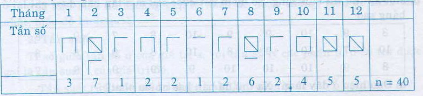
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Tần số | 3 | 5 | 8 | 6 | 2 | 1 | 4 | 9 | 5 | 6 | 3 | 5 | N = 57 |

a,
| giá trị (x) | 10 | 13 | 15 | 17 | |
| tần số (n) | 3 | 4 | 7 | 6 | N=20 |
M0=15 (mốt của dấu hiệu là 15)
b,
X=10.3+13.4+15.7+17.6/20=192,1
a) Áp dụng định lý Pitago vào tam giác AHB, ta có:
=> AB2 = AH2 + BH2
=> BH2 = 152 - 122
BH2 = 32
=> BH = 9 cm
Áp dụng định lý Pitago vào tam giác AHC, ta có:
=> AC2 = AH2 + CH2
=> AC2 = 122 + 162
AC2 = 202
=> AC = 20 cm
BC = BH + HC
BC = 6 + 15
BC = 21 cm
b) Ta có:
AB2 + AC2 = 152 + 202 = 252 = 625
BC2 = 212 = 441
vì 625 khác 441 nên tam giác ABC không vuông

Vì x và y là hai đại lượng tỉ lệ nghịch nên: a = xy = -2. (-15) = 30
Ta có kết quả sau:
|
x |
-2 |
-1 |
1 |
2 |
3 |
5 |
|
y |
-15 |
-30 |
30 |
15 |
10 |
6 |
Vì x và y là hai đại lượng tỉ lệ nghịch nên: a = xy = -2. (-15) = 30
Ta có kết quả sau:
|
x |
-2 |
-1 |
1 |
2 |
3 |
5 |
|
y |
-15 |
-30 |
30 |
15 |
10 |
6 |

a. Dấu hiệu: Thời gian làm bài tập của 30 học sinh.
b.
| Giá trị (x) | 5 | 7 | 8 | 9 | 10 | 14 | |
| Tần số (n) | 4 | 3 | 8 | 8 | 4 | 3 | N = 30 |
Nhận xét:
- Có 4 học sinh làm bài nhanh nhất (3 phút).
- Có 3 học sinh làm bài lâu nhất (14 phút).
- Số học sinh làm bài trong 8, 9 phút chiếm đa số.
c.
x = \(\frac{5\times4+7\times3+8\times8+9\times8+10\times4+14\times3}{30}\)
\(\approx\)8,63
Mốt của dấu hiệu là: Mo = 8 và 9
a/ Dấu hiệu ở đây là thời gian giải một bài toán (tính bằng phút) của 30 học sinh
b/ Lập bảng tần số
| giá trị (x) | 5 | 7 | 8 | 9 | 10 | 14 | |
| tần số (n) | 4 | 3 | 8 | 8 | 4 | 3 | N=30 |
* nhận xét
- Thời gian làm bài ít nhất là 5 phút (có 4 học sinh)
- Thời gian làm bài nhiều nhất là 14 phút ( có 3 học sinh)
- thời gian làm bài nhiều nhất là 14 phút (có 8 học sinh)
c/ tính trung bình cộng
\(\)\(X=\frac{5.4+7.3+8.8+9.8+10.4+14.3}{30}\approx8,63\)
VẬY số trung bình cộng là 8,63
bài toán có hai mốt: M0=8 & M0=9
d/ tự vẽ
e/ Khi mỗi giá trị của dấu hiệu đều giảm 1,5 lần thì số TBC mới giảm 1,5 lần
Nếu mỗi giá trị của dấu hiệu tăng 2 đơn vị thì số TBC tăng thêm 2 đơn vị

x=0 nha bạn
xin lỗi vì làm hơi tắt. Bạn chỉ cần tìm n bằng cách lấy N trừ cho các tần số còn lại rồi làm ra liền

Ta có:
| Giá trị (x) | Tần số (n) | x.n | |
| 7 | 1 | 7 | |
| 9 | x | 9x | |
| 9 | 10 | 90 | |
| 10 | 4 | 40 | |
| N=15+x | Tổng =137+9x | X = 8,85 |
Mặt khác:
X=\(\frac{137+9x}{15+x}\) =8,85
\(\Rightarrow\)137+9x=(15+x).8,85
\(\Rightarrow\)137+9x=8,85.15+8,85.x
\(\Rightarrow\) 137+9x=132,75+8,85.x
Ta có:
| Giá trị (x) | Tần số (n) | x.n | |
| 7 | 1 | 7 | |
| 9 | x | 9x | |
| 9 | 10 | 90 | |
| 10 | 4 | 40 | |
| N=15+x | Tổng =137+9x | X = 8,85 |
Mặt khác:
X=\(\frac{137+9x}{15+x}\)=8,85
⇒137+9x=(15+x).8,85
⇒137+9x=8,85.15+8,85.x
⇒ 137+9x=132,75+8,85.x
 .
.
a. Dấu hiệu là Thời gian giải xong một bài toán (tính bằng phút) của mỗi học sinh lớp 7
b Bảng tần số
M\(_0=15\)
c. Số trung bình cộng thời gian giải xong một bài toán của mỗi học sinh lớp 7 là
X=\(\dfrac{\left(10.3\right)+\left(13.4\right)+\left(15.7\right)+\left(17.6\right)}{20}\)= \(\dfrac{289}{20}\)=14,45
d. Biểu đồ đoạn thẳng: