Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Với m=6 thì phương trình (1) có dạng
x^2 - 5x +4= 0
<=> (x-1)(x-4)=0
<=> x=1 hoặc x=4
Vậy m=6 thì phương trình có nghiệm x=1 hoặc x=4
b. Xét \(\text{ Δ}=\left(-5\right)^2-4\cdot1\cdot\left(m-2\right)=33-4m\)
Để (1) có nghiệm phân biệt khi \(m< \dfrac{33}{4}\)
Theo Vi-et ta có: \(x_1x_2=m-2;x_1+x_2=5\)
Để 2 nghiệm phương trình (1) dương khi m>2
Ta có:
\(\dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}}=\dfrac{3}{2}\Leftrightarrow\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{2}{\sqrt{x_1x_2}}=\dfrac{9}{4}\\ \Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}+\dfrac{2}{\sqrt{x_1x_2}}=\dfrac{9}{4}\\ \Leftrightarrow\dfrac{5}{m-2}+\dfrac{2}{\sqrt{m-2}}=\dfrac{9}{4}\Leftrightarrow20+8\sqrt{m-2}=9\left(m-2\right)\\ \Leftrightarrow\left(\sqrt{m-2}-2\right)\left(9\sqrt{m-2}+10\right)=0\Leftrightarrow\sqrt{m-2}=2\Leftrightarrow m-2=4\Leftrightarrow m=6\left(t.m\right)\)

a. thay m=-4 vào (1) ta có:
\(x^2-5x-6=0\)
Δ=b\(^2\)-4ac= (-5)\(^2\) - 4.1.(-6)= 25 + 24= 49 > 0
\(\sqrt{\Delta}=\sqrt{49}=7\)
x\(_1\)=\(\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+7}{2}\)=6
x\(_2\)=\(\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-7}{2}\)=-1
vậy khi x=-4 thì pt đã cho có 2 nghiệm x\(_1\)=6; x\(_2\)=-1

a, \(x^2-4x+3=0\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x\left(x-1\right)-3\left(x-1\right)=0\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
Vậy tập nghiệm của phương trình là S = { 1 ; 3 }
b, Ta có : \(\Delta=\left(2m+2\right)^2-4\left(2m-5\right)=4m^2+8m+4-8m+20=4m^2+24>0\forall m\)
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m-2\\x_1x_2=\frac{c}{a}=2m-5\end{cases}}\)
Ta có : \(\left(x_1^2-2mx_1-x_2+2m-3\right)\left(x_2^2-2mx_2-x_1+2m-3\right)=19.1=1.19\)
TH1 : \(\hept{\begin{cases}x_1^2-2mx_1-x_2+2m-3=19\\x_2^2-2mx_2-x_1+2m-3=1\end{cases}}\)
Lấy phương trình (1) + (2) ta được :
\(x_1^2+x_2^2-2mx_1-2mx_2-x_2-x_1+4m-6=20\)
mà \(\left(x_1+x_2\right)^2=4m^2+8m+4\Rightarrow x_1^2+x_2^2=4m^2+8m+4-2x_1x_2\)
\(=4m^2+8m+4-2\left(2m-5\right)=4m^2+4m-6\)
\(\Leftrightarrow4m^2+4m-6-2m\left(2m-2\right)-\left(2m-2\right)+4m-6=20\)
\(\Leftrightarrow4m^2+4m-6-4m^2+4m-2m+2+4m-6=20\)
\(\Leftrightarrow10m=30\Leftrightarrow m=3\)tương tự với TH2, nhưng em ko chắc lắm vì dạng này em chưa làm bao giờ

a: Thay m=-5 vào (1), ta được:
\(x^2+2\left(-5+1\right)x-5-4=0\)
\(\Leftrightarrow x^2-8x-9=0\)
=>(x-9)(x+1)=0
=>x=9 hoặc x=-1
b: \(\text{Δ}=\left(2m+2\right)^2-4\left(m-4\right)=4m^2+8m+4-4m+16=4m^2+4m+20>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
\(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=-3\)
\(\Leftrightarrow x_1^2+x_2^2=-3x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow\left(2m+2\right)^2+m-4=0\)
\(\Leftrightarrow4m^2+9m=0\)
=>m(4m+9)=0
=>m=0 hoặc m=-9/4

(a) Khi \(m=2,\left(1\right)\Leftrightarrow x^2-4x-5=0\left(2\right)\).
Phương trình (2) có \(a-b+c=1-\left(-4\right)+\left(-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=5\end{matrix}\right.\).
Vậy: Khi \(m=2,S=\left\{-1;5\right\}\).
(b) Điều kiện: \(x_1,x_2\ne0\Rightarrow m\in R\)
Phương trình có nghiệm khi:
\(\Delta'=\left(-m\right)^2-1\cdot\left(-m^2-1\right)\ge0\)
\(\Leftrightarrow2m^2+1\ge0\left(LĐ\right)\)
Suy ra, phương trình (1) có nghiệm với mọi \(m\).
Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1x_2=\dfrac{c}{a}=-m^2-1\end{matrix}\right.\)
Theo đề: \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=-\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{x_1^2+x_2^2}{x_1x_2}=-\dfrac{5}{2}\Leftrightarrow\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=-\dfrac{5}{2}\)
\(\Leftrightarrow2\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow2\left(2m\right)^2+\left(-m^2-1\right)=0\)
\(\Leftrightarrow7m^2=1\Leftrightarrow m=\pm\dfrac{\sqrt{7}}{7}\) (thỏa mãn).
Vậy: \(m=\pm\dfrac{\sqrt{7}}{7}.\)
bạn giải thích kĩ hộ mik vói cái <=> cuối cùng sao ra như vậy
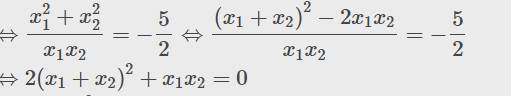

a) Thay m = -12 vào phương trình (1), ta được:
x² - 5x - 12 - 2 = 0
x² - 5x - 14 = 0
Ta có thể phân tích phương trình trên như sau:
x² - 7x + 2x - 14 = 0
x(x - 7) + 2(x - 7) = 0
(x - 7)(x + 2) = 0
Vậy, phương trình có hai nghiệm: x₁ = 7
x₂ = -2
Để phương trình (1) có hai nghiệm phân biệt x₁, x₂, điều kiện là Δ > 0, trong đó Δ là biệt thức của phương trình bậc hai.
Δ = b² - 4ac = (-5)² - 4(1)(m - 2) = 25 - 4m + 8 = 33 - 4m
Để phương trình có hai nghiệm phân biệt, ta cần:
33 - 4m > 0
4m < 33
m < 33/4
Theo hệ thức Viète, ta có:
x₁ + x₂ = -b/a = 5
x₁x₂ = c/a = m - 2
Theo đề bài, ta có:
2(1/x₁ + 1/x₂) = 3
2(x₂ + x₁)/(x₁x₂) = 3
2(5)/(m - 2) = 3
10 = 3(m - 2)
10 = 3m - 6
3m = 16
m = 16/3