Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức đường đi của sự rơi tự do
s = \(\Rightarrow\) t =
với s = h = 20m; g = 10 m/s2.
\(\Rightarrow\) t = √22 s \(\Rightarrow\) t = 2s
Chọn B.
Áp dụng công thức đường đi của sự rơi tự do
s = => t =
với s = h = 20m; g = 10 m/s2.
=> t = √22 s => t = 2s
Chọn B.

Áp dụng CT: \(t=\sqrt{\dfrac{2h}{g}}\)
Theo đề bài có: \(2=\sqrt{\dfrac{2h}{g}}\) \(\Rightarrow\sqrt{\dfrac{2.9h}{g}}=2.\sqrt[]{9}=6\Rightarrow D\)

Chọn B.
Gọi t là thời gian vật rơi hết độ cao h.
Ta có:
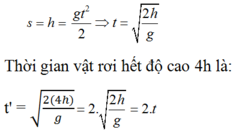
Vì vật rơi từ độ cao h xuống đất hết 1s nên suy ra t' = 2.1 = 2s.

Phương trình chuyển động của viên đá ở các vị trí độ cao là
\(x_h=\dfrac{1}{2}a\cdot0,5^2\)
\(x_H=\dfrac{1}{2}a\cdot1,5^2\)
Ta có\(\dfrac{x_h}{x_H}=\dfrac{\dfrac{1}{2}a\cdot0,5^2}{\dfrac{1}{2}a\cdot1,5^2}=\dfrac{1}{9}\Rightarrow\dfrac{h}{H}=\dfrac{1}{9}\Rightarrow H=9h\)
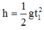
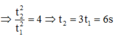
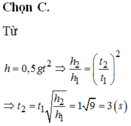
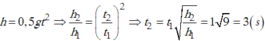
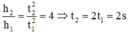

Ta có: h = \(\dfrac{1}{2}\).g.t2 ⇒ t = \(\sqrt{\dfrac{2h}{g}}\) = 1
h' = \(\dfrac{1}{2}\).g.t'2 ⇒ t' = \(\sqrt{\dfrac{2h'}{g}}\) = \(\sqrt{\dfrac{2.4h}{g}}\) = 2.
Vậy đáp án đúng là B.