Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi a (km/h) là vận tốc lên dốc (theo gt vận tốc lên dốc đi và về = nhau ) (a > 0).
Gọi b (km/h) là vận tốc lên dốc (theo gt vận tốc xuống dốc đi và về = nhau ) (b > 0).
Theo đề bài ta có HPT: 4/a + 5/b = 40 5/a + 4/b = 41
Giải hệ (đặt ẩn phụ) ta được a = 1/5, b = 1/4.
Vậy vận tôc lên dốc là 1/5 km/h, xuống dốc là 1/4 km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 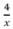 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 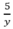 (h)
(h)
Theo đầu bài thời gian đi A đến B là 40 phút = 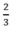 h nên:
h nên:
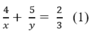
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 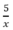 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 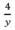 (h)
(h)
Theo đầu bài thời gian đi A đến B là 41 phút = 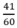 h nên:
h nên:
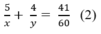
Từ (1) và (2) ta có hệ phương trình:
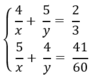
Đặt 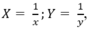 hệ phương trình trên trở thành:
hệ phương trình trên trở thành:
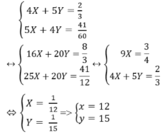
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 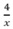 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 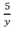 (h)
(h)
Theo đầu bài thời gian đi A đến B là 40 phút = 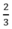 h nên:
h nên:
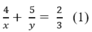
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 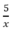 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 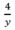 (h)
(h)
Theo đầu bài thời gian đi A đến B là 41 phút = 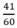 h nên:
h nên:
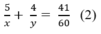
Từ (1) và (2) ta có hệ phương trình:
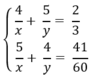
Đặt 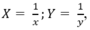 hệ phương trình trên trở thành:
hệ phương trình trên trở thành:
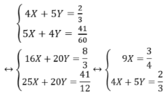
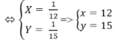
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Cho tam giác ABC, kẻ AH vuông góc với BC (H thuộc BC). Trên mặt phẳng bờ AC không chứa điểm B vẽ Cx // AB; trên tia Cx lấy điểm D sao cho CD = AB
a) Biết góc ABC = 60 độ, tính góc BAH
b) Chứng minh tam giác ABC=tam giác CDA
c) Chứng minh AD vuông góc AH
Bài 1 :
Gọi vận tốc lên dốc và xuống dốc của xe lần lượt là x (km/h) và y (km/h).
Khi đó, thời gian lên dốc và xuống dốc khi đi lần lượt là \(\frac{4}{x}\left(h\right)\) và \(\frac{5}{y}\left(h\right)\)
Do thời gian đi là \(40'=\frac{2}{3}h\) và thời gian về là \(41'=\frac{41}{60}h\) nên ta có hệ
\(\hept{\begin{cases}\frac{4}{x}+\frac{5}{y}=\frac{2}{3}\\\frac{5}{x}+\frac{4}{y}=\frac{41}{60}\end{cases}}\)
Vậy \(\frac{1}{x}=\frac{1}{12},\frac{1}{y}=\frac{1}{15}\)
Suy ra x=12,y=15
Vậy vận tốc lên dốc là 12km/h, vận tốc xuống dốc là 15km/h

bạn đăng tách ra cho mn giúp nhé
Bài 20
Gọi số sản phẩm đc giao của 2 tổ lần lượt là a ; b ( a ; b > 0 )
Theo bài ra ta có hệ \(\left\{{}\begin{matrix}a+b=600\\\dfrac{18a}{100}+\dfrac{21b}{100}=120\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=200\\b=400\end{matrix}\right.\left(tm\right)\)

Gọi x (km) là độ dài quãng đường AM (x > 0)
Gọi y (km) là độ dài quãng đường BM (y > 0)
Thời gian đi từ A đến B: \(\dfrac{x}{9}+\dfrac{y}{18}=2\) (1)
Thời gian đi từ B về A: \(\dfrac{x}{18}+\dfrac{y}{9}=3\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{x}{9}+\dfrac{y}{18}=2\\\dfrac{x}{18}+\dfrac{y}{9}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=36\\x+2y=54\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+2y=72\\x+2y=54\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=18\\2x+y=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\left(nhận\right)\\2.6+y=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\left(nhận\right)\\y=24\left(nhận\right)\end{matrix}\right.\)
Vậy AM = 6 km, MB = 24 km

Giống bài tui cần nhờ nên chấm phát để có thông báo