Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ gọi t1 là thời gian ô tô chạy 1/3 quãng đường đầu
=> t1 = s / ( 3 * v1 ) = s / 120
gọi t2 là thời gian ô tô chạy 1/3 quãng đường tiếp theo
=> t2 = s / ( 3 * v2 ) = s / 150
gọi t3 là thời gian ô tô chạy 1/3 quãng đường cuối cùng
=> t3 = s / ( 3 * v3 )
ta có v tb = s / t = s / ( s / 120 + s / 150 + s / ( 3 *v3) )
=> 45 = s / [s ( 1/ 120 + 1/ 150 + 1/ ( 3 *v3 ) ) ]
=> 45 = 1 / ( 3 / 200 + 1 / ( 3 * v3 )
=> 1 / 45 = 3 / 200 + 1/ ( 3 * v3 )
=> 1 / ( 3 *v3 ) = 1 / 45 - 3 / 200
=> 1 / ( 3 *v3 ) = 13 / 1800
=> 3 * v3 = 1800 / 13
=> v3 = 1800 / 39 = khoảng 46,15 km / h
2/Tính vận tốc trung bình của xe đi từ A đến B
vtb = s/t
theo bài ra ta có : s/2 = 20*t1 và s/2 = 60*t2
=> vtb = s/( t1 + t2) = s/ ( s/40 + s/ 120 ) = 30 (km/h)
Tính vận tốc trung bình của xe đi từ B đến A
theo bài ra ta cũng có
t/2 = s1/20 và t/2 = s2/60
=> vtb" = (s1 + s2 )/t = ( 10t + 30t )/t = 40 ( km/h)
Mà nếu xe từ B xuất phát muộn hơn so với xe xuất phát từ A 30phút = 1/2 h thì 2 xe đến địa điểm cùng 1 lúc
=> sA-B = 30*t
sB-A = 40 * ( t - 1/2)
Mà sA-B = sB-A => 30*t = 40 * ( t - 1/2) => t= 2 (h)
Vậy s = 60 ( km)

Gọi độ dài đoạn Ab là x(km).Gọi các đoạn(đi với vận tõc khác nhau) lần lượt là I,II,III.
Thời gian đi được trong đoạn I:
t1=s1/v1=(1/2x)/60=x/120h
Thời gian đi đoạn II:
t2=s2/v2=(1/4x)/40=x/160h
Thời gian đi đoạn III:
t3=s3/v3=(1/4x)/20=x/80h
Vận tốc trung bình trên cả đoạn đường AB(km/h)
V=(s1+s2+s3)/(t1+t2+t3)
=x/(x/120+x/160+x/80)
=x/[x/40.(1/3+1/4+1/2)]
=x/(13x/480)=480/13
=37km/h
gọi thời gian, vận tốc, nửa đoạn đường đầu lần lượt là t1, v1 , S1
gọi nửa đoạn đường sau là S2
gọi nửa thời gian đầuvà sau của nửa đoạn đường còn lại là t2 và t3
gọi vận tốc của nửa đoạn đường sau trong hai giai đoạn là v2 và v3
ta có :
vtb = \(\frac{S1+S2}{t1+t2+t3}\) =\(\frac{S}{t1+t2+t3}\) =\(\frac{S}{\frac{S1}{v1}+\frac{S2}{v2+v3}}\) =\(\frac{S}{\frac{S}{\frac{2}{v1}}+\frac{S}{\frac{2}{v2+v3}}}\) =\(\frac{S}{\frac{S}{2v1}+\frac{S}{2.\left(v2+v3\right)}}\) = \(\frac{S}{S.\left(\frac{1}{2.60}+\frac{1}{2.\left(40+20\right)}\right)}\) =\(\frac{1}{\frac{1}{120}+\frac{1}{120}}\) =\(\frac{1}{\frac{2}{120}}\) = 60 km/h

a, Gọi thời gian xe đi trên cả guãng đường là t(h)
Quãng đường xe đi được trong nửa thời gian đầu là:
S1=1/2.t.v1=1/2.t.60=t.30(km)
Quãng đường xe đi được trong nửa thời gian sau là:
S2=1/2.t.v2=1/2.t.18=t.9(km)
Vận tốc trung bình của xe trên cả quãng đường là:
vtb=(S1+S2)/t=(30t+9t)/t=39(km/h)
b, Gọi chiều dài quãng đường là S(km)
Thời gian để xe đi quãng nửa quãng đường đầu là:
t1=1/2.S/v1=1/2.S/12=S/24(h)
Thời gian để xe đi nửa quãng đường sau là:
t2=1/2.S/v2=1/2.S/12=s/24(km/h)
Vận tốc trung bình của xe trên cả quãng đường là:
vtb=S/(t1+t2)=S(S/24+S/24)=S/[S(1/24+1/24)]=12(km/h)
c, Gọi S là chiều dài quãng đường AB t là thời gian xe đi hết nửa guãng đường sau
Thời gian xe đi hết nửa quãng đường đầu là:
t1=1/2.S:60=S/120(h)
Quãng đường xe đi được trong thời gian t là:
S'=1/2.t.40+1/2.t.20=20.t+10.t=30.t(km)
Ta có S'=1/2S=>S=60.t
Vận tốc trùng bình của xe là:
vtb=S/(t1+t)=60.t/[(60.t)/120+t]=60.t/(t/2+t)=60.t/1,5t=40(km/h)

a)
- Chọn gốc tọa độ O là vị trí ô tô bắt đầu đuổi theo xe khách và mốc thời gian là thời điểm ô tô đang ở O.
- Phương trình chuyển động của hai xe là:
+ Ô tô: \(x_1=v_1.t=60t\)
+ Xe khách: \(x_2=x_0+v_2.t=20+40t\)b) - Lập bảng biến thiên (tớ làm cái này chứ ít thấy người viết cái này bạn nhé)
| \(t\left(h\right)\) | \(0\) | \(1\) |
| \(x_1\left(km\right)\) | \(0\) | \(60\) |
| \(x_2\left(km\right)\) | \(20\) | \(60\) |
=> Ta vẽ được đồ thị của 2 xe như sau:

c) Dựa vào đồ thị cho ta biết thời điểm 2 xe gặp nhau là sau 1 giờ và tại vị trí có toạ độ \(60km\)
Bạn chưa tính x thì làm sao lập đồ thị được, bảng biến thiên có bị thiếu ko, thấy hơi kì
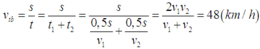
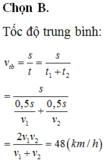

a và c sai rồi