*Dạng 2: Các bài toán liên quan đến hệ pt, phương trình bậc hai một ẩn và áp dụng hệ thức Vi-et Bài 1 : Cho phương trình :x2 – mx + 2(m – 2 ) = 0 a/ Giải phương trình khi m = 1 b/ Chứng minh rằng phương trình luôn có nghiệm với mọi m c/ Tìm m để phương trình có hai nghiệm 2x1 + 3x 2 = 5 Bài 2: Cho phương trình . Giải phương trình khi m =2 Tìm các giá trị của m để phương trình có nghiệm. Gọi...
Đọc tiếp
*Dạng 2: Các bài toán liên quan đến hệ pt, phương trình bậc hai một ẩn và áp dụng hệ thức Vi-et
Bài 1 : Cho phương trình :x2 – mx + 2(m – 2 ) = 0
a/ Giải phương trình khi m = 1
b/ Chứng minh rằng phương trình luôn có nghiệm với mọi m
c/ Tìm m để phương trình có hai nghiệm 2x1 + 3x 2 = 5
Bài 2: Cho phương trình  .
.
Giải phương trình khi m =2
Tìm các giá trị của m để phương trình có nghiệm.
Gọi  là hai nghiệm của phương trình. Tìm giá trị của m để:
là hai nghiệm của phương trình. Tìm giá trị của m để: 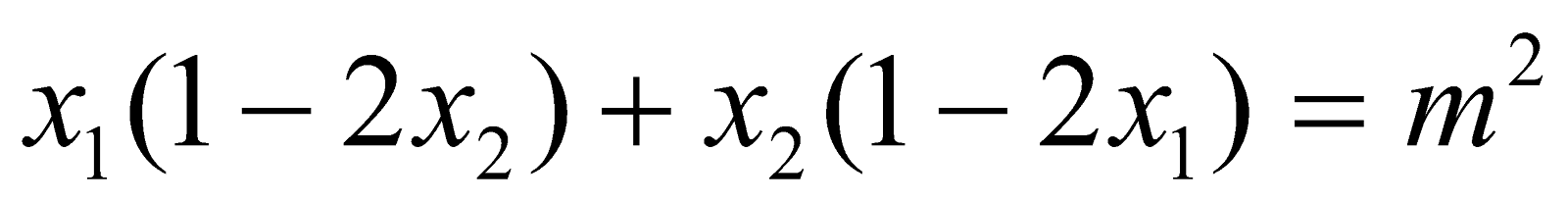
Bài 3: Cho phương trình: 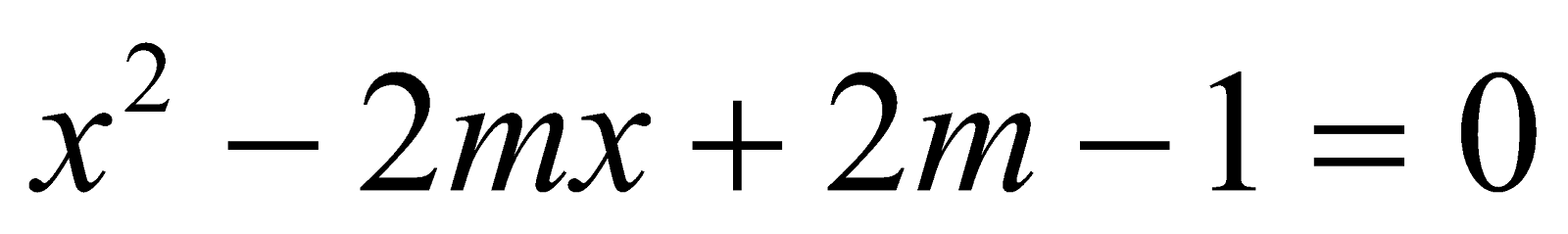
a) Chứng tỏ rằng phương trình có nghiệm  với mọi m.
với mọi m.
b) Đặt A= .
.
b1) Chứng minh rằng: A=
b2) Tìm m sao cho A= 27.
c) Tìm m sao cho phương trình có nghiệm này bằng ba lần nghiệm kia
Bài 4: Cho phương trình bậc hai x2 – 2(m + 1) x + m – 4 = 0 (1)
a/ Giải phương trình (1) khi m = 1
b/ Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi m
c/ Chứng minh rằng : Biểu thức A = x1 (1 – x2) + x2( 1 – x1 ) không phụ thuộc vào giá trị của m


a) \(=\sqrt{\left(3-\sqrt{7}\right)^2}+\sqrt{7}=3-\sqrt{7}+\sqrt{7}=3\)
b) \(=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{5}-\sqrt{2}}+\dfrac{6\left(2+\sqrt{10}\right)}{4-10}+\sqrt{10}-2\)
\(=\sqrt{3}-2-\sqrt{10}+\sqrt{10}-2=-4+\sqrt{3}\)