Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??

Bài 1
a. (Tự vẽ hình)
Áp dụng định lí Py-ta-go, ta có:
BC2= AB2 + AC2
<=> BC2= 62 + 82
<=> BC2= 100
=> BC = 10 (cm)
Bài 1
b. Áp dụng định lí Py-ta-go, ta có:
AC2 = AH2 + HC2
<=> 82 = 4,82 + HC2
<=> 64 = 23,04 + HC2
=> HC2 = 64 - 23,04
=> HC2 = 40,96
=> HC = 6,4 (cm)
=> HB = BC - HC = 10 - 6,4 = 3,6 (cm)

A C B D M
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.

Answer:
Bài 1:
Vì AB = AC nên tam giác ABC cân tại A
=> Góc ABC = góc ACB = (180 độ - góc BAC) : 2 = 30 độ
Ta gọi DF là trung trực của AC
=> DF vuông góc AC = F; FC = FA
Mà DF là trung trực của AC
=> Góc ADA = 2 góc CDF = 2 . (180 độ - góc DCF - góc CFD) = 120 độ
Xét tam giác ACE và tam giác BAD:
BD = AE
AC = AB
Góc EAC = góc DBA = 30 độ
=> Tam giác ACE = tam giác BAD (c.g.c)
=> Góc CED = góc ADB = góc EDC = 180 độ - góc CDA = 60 độ
Bài 2:
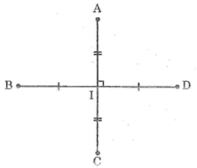
Có: IK là trung trực của BC
=> IB = IC
Tương tự ID = IA mà AB = CD
=> Tam giác IAB = tam giác IDC (c.c.c)
=> Góc IAB = góc IDA = góc IAC
=> AI là tia phân giác của góc BAD
Mà AI là tia phân giác của góc A
IE vuông góc AB; IH vuông góc AC
=> IE = IH
\(\Rightarrow BE^2=IB^2-IE^2=IC^2-IH^2=HC^2\)
=> BE = HC
Mà IE = IH; góc IEA = góc IHA = 90 độ; góc EAI = góc IAH
=> Tam giác AEI = tam giác AHI (g.c.g)
=> AE = AH mà IE = IH
=> IA là trung trực của EH
Có: CF song song AB nên góc FHC = góc AHE = góc AEH = góc HFC
=> Tam giác CHF cân ở C
=> CF = CH
=> CF = BE
Mà KB = KC; góc EBK = góc KCF
=> Tam giác BKE = tam giác CKF (c.g.c)
=> Góc BKE = góc FKC
=> E, F, K thẳng hàng

Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm


b.
Trên tia đối của MA lấy điểm N sao cho MA=MN.
Kẻ \(DF\perp AM\left(F\in AM\right)\)
Tí nữa tớ hướng dẫn cho
a: Xét tứ giác ACBD có
O là trung điểm của AB
O là trung điểm của CD
Do đó: ACBD là hình bình hành
Suy ra: AD//BC và AC//BD