
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


giải như thế này
a) Số bút trong mỗi hộp là a và giả sử Mai đã mua x hộp được 28 bút. Do đó 28=a.x; nghĩa là a là một ước của 28. Tương tự, Lan đã mua 36 bút nên a cũng là một ước của 36. Hơn nữa a>2.
b) Theo câu a) thì a là một ước chung của 28 và 36.
Ta có:
28=22.7,
36=22.32.
ƯCLN(28,36)=22=4. Do đó ƯC(28,36)={1;2;4}.
Vì a là một ước chung và lớn hơn 2 nên a=4.
c) Gọi số hộp bút Mai đã mua là x và 4.x=28 nên x=28:4=7.
Gọi số hộp bút Lan đã mua là y, ta có 4.y=36. Do đó y=36:4=9.
Vậy Mai đã mua 7 hộp, Lan đã mua 9 hộp.
k mik nha

Tìm ƯCLN rồi tìm các ước chung của:
a) 16 và 24; b) 180 và 234; c) 60, 90, 135.
Bài giải:
a) ƯCLN (16, 24) = 8, ƯC (16, 24) = {1; 2; 4; 8};
b) Ta có 180 = 22 . 32 . 5; 234 = 2 . 32 . 13;
ƯCLN (180, 234) = 2 . 32 = 18, ƯC (180, 234) = {1; 2; 3; 6; 9; 18};
c) Ta có 60 = 22 . 3 . 5; 90 = 2 . 32 . 5; 135 = 33 . 5. Do đó
ƯCLN (60, 90, 135) = 3 . 5 = 15; ƯC (60, 90, 135) = {1; 3; 5; 15}.
Các thông tin cần biết khi tham gia Giúp tôi giải toán
"Giúp tôi giải toán" trên Online Math đã trở thành một diễn đàn hết sức sôi động cho các bạn học sinh, các thầy cô giáo và các bậc phụ huynh từ mọi miền đất nước. Ở đây các bạn có thể chia sẻ các bài toán khó, lời giải hay và giúp nhau cùng tiến bộ. Để diễn đàn này ngày càng hữu ích, các bạn lưu ý các thông tin sau đây:
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các bài toán hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
II. Cách nhận biết câu trả lời đúng
Trên diễn đàn có thể có rất nhiều bạn tham gia giải toán. Vậy câu trả lời nào là đúng và tin cậy được? Các bạn có thể nhận biết các câu trả lời đúng thông qua 6 cách sau đây:
1. Lời giải rõ ràng, hợp lý (vì nghĩ ra lời giải có thể khó nhưng rất dễ để nhận biết một lời giải có là hợp lý hay không. Chúng ta sẽ học được nhiều bài học từ các lời giải hay và hợp lý, kể cả các lời giải đó không đúng.)
2. Lời giải từ các giáo viên của Online Math có thể tin cậy được (chú ý: dấu hiệu để nhận biết Giáo viên của Online Math là các thành viên có gắn chứ "Quản lý" ở ngay sau tên thành viên.)
3. Lời giải có số bạn chọn "Đúng" càng nhiều thì càng tin cậy.
4. Người trả lời có điểm hỏi đáp càng cao thì độ tin cậy của lời giải sẽ càng cao.
5. Các bài có dòng chữ "Câu trả lời này đã được Online Math chọn" là các lời giải tin cậy được (vì đã được duyệt bởi các giáo viên của Online Math.)
6. Các lời giải do chính người đặt câu hỏi chọn cũng là các câu trả lời có thể tin cậy được.
III. Thưởng VIP cho các thành viên tích cực
Online Math hiện có 2 loại giải thưởng cho các bạn có điểm hỏi đáp cao: Giải thưởng chiếc áo in hình logo của Online Math cho 3 - 5 bạn có điểm hỏi đáp cao nhất trong tháng và giải thưởng 1 tháng VIP cho 3 - 5 bạn có điểm hỏi đáp cao nhất trong tuần. Thông tin về các bạn được thưởng tiền được cập nhật thường xuyên tại đây.

a,
+ Nếu t = 12 tức là nhiệt đô tăng 120C
+ Nếu t = -3 thì tức là nhiệt độ giảm 30C
+ Nếu t = 0 thì tức là nhiệt độ không đổi
b, + Nếu a = 70 tức là số tiền tăng 70000đ
+ Nếu a = -500 tức là số tiền giảm 500000đ
+ Nếu a = 0 tức à số tiền giữ nguyên

bài 48
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy
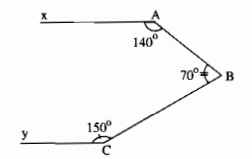
Giải
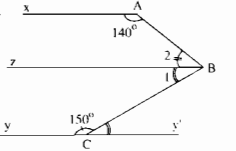
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
bài 49
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy

Giải

Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy


\(2M=\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{12-10}{10.11.12}=\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}-\frac{1}{11.12}=\frac{1}{2}-\frac{1}{11.12}\)
\(\Rightarrow M=\frac{1}{4}-\frac{1}{11.24}=\frac{66-1}{11.24}=\frac{65}{11.24}\)
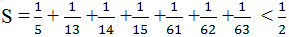
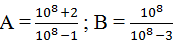
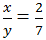
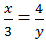
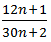 là phân số tối giản (n ∈ N)
là phân số tối giản (n ∈ N)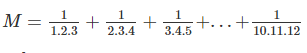
bai gi ma ki zay
trong sach toan lop tap 1 y