Question

[pikachu(^_^)]

Bài 1: Tìm chu kỳ tuần hoàn của hàm số sau:

a) y= cos\(^2\)x                                       

Answer 1

[Ngô Thành Chung]

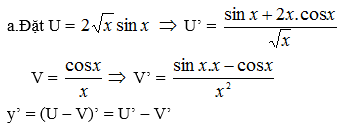
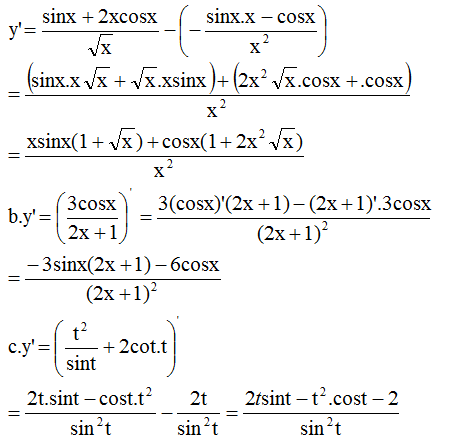
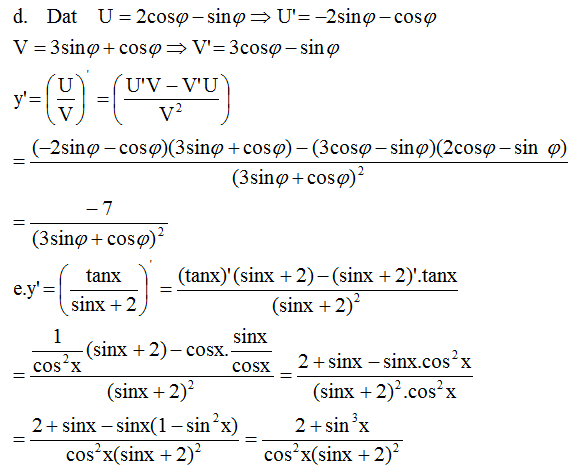
Ta có cos²(x + π) = [-cosx]² = cos²x

Giả sử tồn tại số T ∈ (0 ; π) thỏa mãn

cos²x = cos²(x + T) với mọi x

⇔ 2cos²x - 1 = 2cos²(x + T) - 1 với mọi x

⇔ cos2x = cos (2x + 2T) với mọi x (1)

(*) : cos2x = cos (2x + 2T)

Thay x = \(\pi\) vào ta được

1 = cos(T + 2π) ⇔ cosT = 1

Do T ∈ (0 ; π) nên cosT ≠ 1.

Vậy x = π không thỏa mãn (*) : cos2x = cos (2x + 2T)

Vậy (1) là mệnh đề sai

Dẫn đến mệnh đề "Giả sử" là sai

Nói cách khác : Không có số T ∈ (0 ; π) thỏa mãn cos²x = cos²(x + T) với mọi x

Tóm lại : T = π là số dương bé nhất thỏa mãn cos²x = cos²(x + T)

nên chu kì của hàm số này là π

Answer 2

[Akai Haruma]

Lời giải:

$y=f(x)=\cos ^2x=\frac{\cos 2x+1}{2}$

Hàm này có chu kỳ $T=\frac{2\pi}{|2|}=\pi$