Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) x≠2x≠2
Bài 2:
a) x≠0;x≠5x≠0;x≠5
b) x2−10x+25x2−5x=(x−5)2x(x−5)=x−5xx2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
c) Để phân thức có giá trị nguyên thì x−5xx−5x phải có giá trị nguyên.
=> x=−5x=−5
Bài 3:
a) (x+12x−2+3x2−1−x+32x+2)⋅(4x2−45

a) xác định khi x khác +-1
b)
\(A=\left(\frac{\left(2x+1\right).\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\frac{8}{\left(x-1\right)\left(x+1\right)}-\frac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\right).\frac{\left(x-1\right)}{\left(x+1\right)}\)
\(A=\left(\frac{\left(2x^2+3x+1\right)+8-\left(x^2-2x+1\right)}{\left(x-1\right)\left(x+1\right)}\right).\frac{\left(x-1\right)}{\left(x+1\right)}=\frac{x^2+5x+8}{\left(x-1\right)\left(x+1\right)}.\frac{x-1}{x+1}\)
\(A=\frac{x^2+5x+8}{\left(x+1\right)^2}=1+\frac{3\left(x+1\right)+4}{\left(x+1\right)^2}\)
c)
GTNN \(B=\frac{3y+4}{y^2}\ge-\frac{9}{16}\)
GTNN \(A=\frac{7}{16}\)

a, ĐKXĐ: \(\hept{\begin{cases}5x+25\ne0\\x\ne0\\x^2+5x\ne0\end{cases}\Rightarrow\hept{\begin{cases}5\left(x+5\right)\ne0\\x\ne0\\x\left(x+5\right)\ne0\end{cases}\Rightarrow}}\hept{\begin{cases}x\ne0\\x\ne-5\end{cases}}\)
b, \(P=\frac{x^2}{5x+25}+\frac{2x-10}{x}+\frac{50+5x}{x^2+5x}\)
\(=\frac{x^3}{5x\left(x+5\right)}+\frac{5\left(2x-10\right)\left(x+5\right)}{5x\left(x+5\right)}+\frac{\left(50+5x\right).5}{5x\left(x+5\right)}\)
\(=\frac{x^3+10\left(x-5\right)\left(x+5\right)+250+25x}{5x\left(x+5\right)}\)
\(=\frac{x^3+10x^2+25x}{5x\left(x+5\right)}=\frac{x\left(x+5\right)^2}{5x\left(x+5\right)}=\frac{x+5}{5}\)
c, \(P=-4\Rightarrow\frac{x+5}{5}=-4\Rightarrow x+5=-20\Rightarrow x=-25\)
d, \(\frac{1}{P}\in Z\Rightarrow\frac{5}{x+5}\in Z\Rightarrow5⋮\left(x+5\right)\Rightarrow x+5\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\Rightarrow x\in\left\{-10;-6;-4;0\right\}\)
Mà x khác 0 (ĐKXĐ của P) nên \(x\in\left\{-10;-6;-4\right\}\)
a) \(ĐKXĐ:\hept{\begin{cases}5x+25\ne0\\x\ne0\\x^2+5x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne-5\end{cases}}\)
b) \(P=\frac{x^2}{5x+25}+\frac{2x-10}{x}+\frac{50+5x}{x^2+5x}\)
\(P=\frac{x^3}{5x\left(x+5\right)}+\frac{10x^2-250}{5x\left(x+5\right)}+\frac{250+25x}{5x\left(x+5\right)}\)
\(P=\frac{x^3+10x^2+25x}{5x\left(x+5\right)}=\frac{x\left(x+5\right)^2}{5x\left(x+5\right)}=\frac{x+5}{5}\)
c) \(P=4\Leftrightarrow\frac{x+5}{5}=4\Leftrightarrow x+5=20\Leftrightarrow x=15\)
d) \(\frac{1}{P}=\frac{5}{x+5}\in Z\Leftrightarrow5⋮x+5\)
\(\Leftrightarrow x+5\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Lập bảng nhé
e) \(Q=P+\frac{x+25}{x+5}=\frac{x+30}{x+5}=1+\frac{25}{x+5}\)
\(Q_{min}\Leftrightarrow\frac{25}{x+5}_{min}\)

a) Điều kiện:
x3 - 8 \(\ne\)0
\(\Leftrightarrow\)(x - 2)(x2 + 2x + 4)\(\ne\)0
\(\Leftrightarrow\hept{\begin{cases}x-2\ne0\\x^2+2x+4\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ne2\\\left(x+1\right)^2+3\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ne2\\\left(x+1\right)^2\ne-3\end{cases}}\)
(vô lí vì (x + 1)2 \(\ge\)0 > -3)
\(\Rightarrow\)x \(\ne\)2
b) \(\frac{3x^2+6x+12}{x^3-8}\)
\(=\frac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\frac{3}{x-2}\)
c) Thế x = \(\frac{4001}{2000}\)vào, ta có:
\(\frac{3x^2+6x+12}{x^3-8}\)
\(=\frac{3}{x-2}\)
\(=\frac{3}{\frac{4001}{2000}-2}\)
\(=\frac{3}{\frac{4001}{2000}-\frac{4000}{2000}}\)
\(=\frac{3}{\frac{1}{2000}}\)
\(=3.2000=6000\)

a.ĐKXĐ \(\hept{\begin{cases}x\ne-3\\x\ne2\end{cases}}\)
A=\(\frac{x+2}{x+3}-\frac{5}{\left(x+3\right)\left(x-2\right)}-\frac{1}{x-2}\)
=\(\frac{\left(x+2\right)\left(x-2\right)-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\frac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}=\frac{\left(x-4\right)\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
=\(\frac{x-4}{x-2}\)
b. Để A >0 thì \(\frac{x-4}{x-2}\) >0 \(\Rightarrow\orbr{\begin{cases}x< 2\\x>4\end{cases}}\)
Kết hợp ĐK thì \(\orbr{\begin{cases}x< 2,x\ne-3\\x>4\end{cases}}\)
c. \(A=\frac{x-4}{x-2}=1+\frac{-2}{x-2}\)
Để A nguyên thì \(x-2\inƯ\left(-2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow x\in\left\{0,1,3,4\right\}\)
Khi thay vào A, để A dương thì \(x\in\left\{0;1\right\}\)
Vậy để A nguyên dương thì \(x\in\left\{0;1\right\}\)
Câu c, có thể nói kết hợp với điều kiện giải được trong câu b, ta tìm được \(x\in\left\{0;1\right\}\)
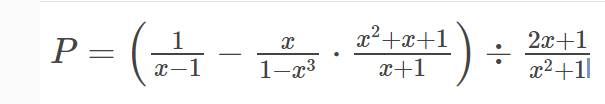
 Câu1:Điền vào...để có hăng đẳng thức đáng nhớ
Câu1:Điền vào...để có hăng đẳng thức đáng nhớ
Câu 1:
\(25\left(x-y\right)^2-16\left(x+y\right)^2\)
\(=\left[5\left(x-y\right)\right]^2-\left[4\left(x+y\right)\right]^2\)
\(=\left(5x-5y\right)^2-\left(4x+4y\right)^2\)
\(=\left(5x-5y-4x-4y\right)\left(5x-5y+4x+4y\right)\)
\(=\left(x-9y\right)\left(9x-y\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{1;-\dfrac{1}{2}\right\}\)
b: \(P=\left(\dfrac{1}{x-1}-\dfrac{x}{1-x^3}\cdot\dfrac{x^2+x+1}{x+1}\right):\dfrac{2x+1}{x^2+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{x+1}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\dfrac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^2+1}{2x+1}=\dfrac{x^2+1}{x^2-1}\)
c: Thay x=1/2 vào P, ta được:
\(P=\dfrac{\left(\dfrac{1}{2}\right)^2+1}{\left(\dfrac{1}{2}\right)^2-1}=\dfrac{5}{4}:\dfrac{-3}{4}=\dfrac{5}{4}\cdot\dfrac{-4}{3}=-\dfrac{5}{3}\)