Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Trong nửa thời gian đầu: S 1 = v 1 . t 1 = 60. t 2 = 30 t
Trong nửa thời gian cuối: S 2 = v 2 . t 2 = 40. t 2 = 20 t
Mà ta có: v t b = S t = S 1 + S 2 t 1 + t 2 = 30 t + 20 t t = 50 k m / h

Vận tốc trung bình của ô tô là:
Ta có: \(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{\dfrac{v_1t}{2}+\dfrac{v_2t}{2}}{t}=\dfrac{v_1+v_2}{2}=\dfrac{60+40}{2}=50\left(km/h\right)\)

I will help :))
A B t1=1/2t t2=1/2t S1 S2
\(S1=v1.t1=60.\frac{1}{2}t=30t\) ( km )
\(S2=v2.t2=40.\frac{1}{2}t=20t\left(km\right)\)
\(AB=S1+S2=30t+20t=50t\)
\(Vtb=\frac{S}{t}=\frac{50t}{t}=50\left(\frac{km}{h}\right)\)
:))
Vận tốc trung bình của ô tô trên cả quãng đường là :
(60 + 40) : 2 = 50 (km/giờ)
Vậy Vận tốc trung bình của ô tô trên cả quãng đường là : 50 km/giờ

a)
- Chọn gốc tọa độ O là vị trí ô tô bắt đầu đuổi theo xe khách và mốc thời gian là thời điểm ô tô đang ở O.
- Phương trình chuyển động của hai xe là:
+ Ô tô: \(x_1=v_1.t=60t\)
+ Xe khách: \(x_2=x_0+v_2.t=20+40t\)b) - Lập bảng biến thiên (tớ làm cái này chứ ít thấy người viết cái này bạn nhé)
| \(t\left(h\right)\) | \(0\) | \(1\) |
| \(x_1\left(km\right)\) | \(0\) | \(60\) |
| \(x_2\left(km\right)\) | \(20\) | \(60\) |
=> Ta vẽ được đồ thị của 2 xe như sau:

c) Dựa vào đồ thị cho ta biết thời điểm 2 xe gặp nhau là sau 1 giờ và tại vị trí có toạ độ \(60km\)
Bạn chưa tính x thì làm sao lập đồ thị được, bảng biến thiên có bị thiếu ko, thấy hơi kì

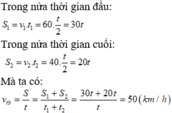


Bài 1
Chọn trục Ox trùng với quỹ đạo , gốc tọa độ O ở A , chiều dương là chiều chuyển động từ A -> B .Mốc thời gian t0=0 lúc xe xuất phát
Quãng đường S1 vật đi được trong thời gian t1 là :
S1 = v1.t1 = 60.1/2t = 30t (km)
Quãng đường S2 vật đi được trong thời gian t2 là :
S2 = v2.t2 = 40.1/2t = 20t ( km)
Gọi vận tốc trung bình của vật trên cả quãng đường AB là \(\overline{v}\)
ta có : \(\overline{v}=\dfrac{S}{t}=\dfrac{S1+S2}{t}=\dfrac{30t+20t}{t}=\dfrac{t\left(50\right)}{t}=50\left(\dfrac{km}{h}\right)\)
Vậy....
Bài 2 :
Chọn trục Ox....
Thời gian t1 để người đi xe đạp đi hết nửa đoạn đường đầu s1 là :
t1 = \(\dfrac{0,5S}{12}\left(h\right)\)
Thời gian t2 để người đi xe đạp đi hết nửa đoạn cuối S2 là :
t2 = \(\dfrac{0,5S}{18}\left(h\right)\)
Gọi vận tốc trung bình của người đi xe đạp trên cả quãng đường là \(\overline{v}\):
ta có : \(\overline{v}=\dfrac{S}{t}=\dfrac{S}{t1+t2}=\dfrac{S}{\dfrac{0,5S}{12}+\dfrac{0,5S}{18}}=\dfrac{S}{0,5S\left(\dfrac{1}{12}+\dfrac{1}{18}\right)}\) = \(\dfrac{1}{0,5\left(\dfrac{1}{12}+\dfrac{1}{18}\right)}=14,4\left(\dfrac{km}{h}\right)\)
vậy...