Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

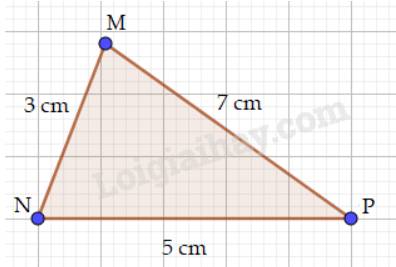
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

a) vì x và y tỷ lệ nghịch voeis nhau nên ta có công thức: x=a/y
=> 4=a/10
=>a=4x10
=>a=40
b) y=40/x
c) nếu x=5 => y=40/5=>y=8
nếu x= -8=> y=40/-8=>y=-5
HT

nếu \(a\perp b\) và b//c thì ta có : \(a\perp c\)
vậy chọn đáp án B

A B C D E K F
a, K;F là trung điểm của BD; BC (gt)
=> FK là đtb của tg BDC
=> FK // DC
mà DC // AB do ABCD là hình thang
=> FK//AB
b, K;E là trung điểm của BD; AD => KE là đtb của tg ABD
=> KE = 1/2 AB VÀ KE // AB
có AB = 4
=> ke = 2 cm
c, có KE // AB mà KF // AB
=> E;K;F thẳng hàng (tiên đề ơ clit)

a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm
Góc đối diện với cạnh `MN` là: `\hat{P}`
Góc đối diện với cạnh `NP` là: `\hat{M}`
Góc đối diện với cạnh `MP` là: `\hat{N}`
Vì: `MN < NP < MP ( 4 < 7 < 9)` nên `\hat{P} < \hat{M} < \hat{N}`
Các góc của tam giác MNP theo thứ tự từ bé đến lớn là: `\hat{P} ; \hat{M}; \hat{N}`
Góc đối diện cạnh MN là \(\widehat{P}\)
Góc đối diện cạnh NP là \(\widehat{M}\)
Góc đối diện cạnh MP là \(\widehat{N}\)
Do \(MN< NP< MP\) nên \(\widehat{P}< \widehat{M}< \widehat{N}\)