Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: \(BC=\sqrt{9^2+12^2}=15\)
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{12}{15}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq37^0\)
b: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{15}{7}\)
Do đó; BD=45/7(cm); CD=60/7(cm)
c: Xét tứ giác AEDF có \(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
nên AEDF là hình chữ nhật
mà AD là phân giác của góc FAE
nên AEDF là hình vuông

a,Trong \(\Delta\) ABH có AHB=900 (BH \(\perp\) BC tại H -gt)
AH2 + BH2 =AB2 (định lý Pi-ta-go)
T/s:162 +252 =AB2
\(\Rightarrow\) AB2 =881
mà AB>0
\(\Rightarrow\) AB=\(\sqrt{881}\)\(\approx\) 29.68
Trong\(\Delta\) ABC có BAC=900 (gt), Đường cao AH (gt)
AH2= BH*CH (hệ thức lượng)
T/s: 162=25*CH
\(\Rightarrow\) CH=\(\dfrac{16^2}{25}\) = 10.24
Có:BH+HC=BC(H\(\in\) BC)
T/s: 25+10.24=BC
\(\Rightarrow\) BC=35.24
Trong \(\Delta\) ABC có:BAC=900 (GT)
AB2 +AC2 =BC2(Định lý Py-ta-go)
T/s:29.682+AC2\(\approx\)35.242
\(\Rightarrow\) AC2\(\approx\)35.242-29.682
\(\approx\)360.95
Mà AC>0
\(\Rightarrow\) AC\(\approx\) 19

\(\sqrt{1-x-2x^2}=\sqrt{\left(1+x\right)\left(1-2x\right)}\le\dfrac{1+x-2x+1}{2}=\dfrac{-x+2}{2}\)
(AM-GM)
do đó \(A\le\dfrac{x}{2}+\dfrac{-x+2}{2}=1\)
Dấu = xảy ra khi 1+x=1-2x <=> x=0 (tmđk)

a) Ta có AMN=MAN=ANM=90=>tứ giác AMHN là hình chữ nhật
=>AMN=HAM
Mà HAM=ACB( cùng cộng với ABC=90độ)
=>AMN=ACB
=>tam giác AMN ~ tam giác ACB
=>........................

\(BC=BH+CH=145\left(cm\right)\)
\(AB=\sqrt{64\cdot145}=8\sqrt{145}\left(cm\right)\)
\(AC=\sqrt{81\cdot145}=9\sqrt{145}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}=\dfrac{8\sqrt{145}}{145}\)
nên \(\widehat{C}\simeq41^0\)
\(\Leftrightarrow\widehat{B}=49^0\)


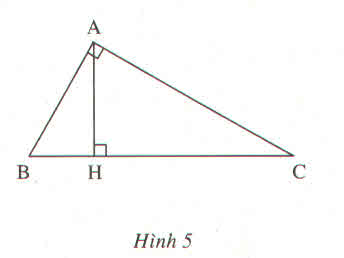
Bài 1.
a. Xét tam giác ABC vuông tại A có AH là đường cao:
\(AH^2=BH.HC\) (HTL)
\(\Rightarrow AH=\sqrt{BH.HC}=\sqrt{25.64}=40\)(đvđd)
b. Xét tam giác ABH vuông tại H có:
\(\tan B=\dfrac{AH}{BH}\) (TSLG)
\(\Rightarrow\tan B=1,6\Rightarrow\widehat{B}=\approx58^0\)
Ta có: \(\widehat{B}+\widehat{C}=90^0\) (tam giác ABC vuông tại A)
\(\Rightarrow\widehat{C}=90^0-\widehat{B}\approx90^0-58^0\approx32^0\)
Bài 2. Kẻ đường cao AH.
Ta có: AB=AC=7cm => tam giác ABC cân tại A.
=> AH cũng là trung tuyến.
=> BH=CH=3cm.
Xét tam giác AHC vuông tại H có:
\(\cos C=\dfrac{CH}{AC}\) (TSGL)
\(\Rightarrow\cos C=\dfrac{3}{7}\Rightarrow\widehat{C}\approx65^0\)
\(\Rightarrow\widehat{B}\approx65^0\) (Tam giác ABC cân tại A)
\(\Rightarrow\widehat{BAC}\approx180^0-2.65^0\approx50^0\)