Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^5-4x^3-5x\)
\(=x\left(x^4-4x^2-5\right)\)
\(=x\left(x^4-5x^2+x^2-5\right)\)
\(=x\left[x^2\left(x^2-5\right)+\left(x^2-5\right)\right]\)
\(=x\left(x^2+1\right)\left(x+\sqrt{5}\right)\left(x-\sqrt{5}\right)\)
a/
\(a^4+b^4+c^4-2a^2b^2-2b^2c^2-2c^2a^2.\)
=>\(a^4+b^4+c^4-2\left(ab\right)^2-2\left(bc\right)^2-2\left(ac\right)^2\)
=>\(a^4+b^4+c^4-2\left(ab\right)^2-2\left(bc\right)^2+2\left(ac\right)^2-4\left(ca\right)^2\)
áp dụng hằng đẳng thức \(a^2-b^2-c^2=a^4+b^4+c^4-2\left(ab\right)^2-2\left(bc\right)^2+2\left(ac\right)^2\) ta đc
\(\left(a^2-b^2+c^2\right)-4\left(ac\right)^2\)
=> \(\left(a^2-b^2+c^2-2ac\right)\left(a^2-b^2+c^2+2ac\right)\)

1. (a2+b2+ab)2-a2b2-b2c2-c2a2
=a4+b4+a2b2+2(a2b2+ab3+a3b)-a2b2-b2c2-c2a2
=a4+b4+2a2b2+2ab3+2a3b-b2c2-c2a2
=(a2+b2)2+2ab(a2+b2)-c2(a2+b2)
=(a2+b2)[(a+b)2-c2]
=(a2+b2)(a+b+c)(a+b-c)
2. a4+b4+c4-2a2b2-2b2c2-2a2c2=(a2-b2-c2)2
3. a(b3-c3)+b(c3-a3)+c(a3-b3)
=ab3-ac3+bc3-ba3+ca3-cb3
=a3(c-b)+b3(a-c)+c3(b-a)
=a3(c-b)-b3(c-a)+c3(b-a)
=a3(c-b)-b3(c-b+b-a)+c3(b-a)
=a3(c-b)-b3(c-b)-b3(b-a)+c3(b-a)
=(c-b)(a-b)(a2+ab+b2)-(b-a)(b-c)(b2+bc+c2)
=(a-b)(c-b)(a2+ab+2b2+bc+c2)
4. a6-a4+2a3+2a2=a4(a+1)(a-1)+2a2(a+1)=(a+1)(a5-a4+2a2)=a2(a+1)(a3-a2+2)
5. (a+b)3-(a-b)3=(a+b-a+b)[(a+b)2+(a+b)(a-b)+(a-b)2]
=2b(3a2+b2)
6. x3-3x2+3x-1-y3=(x-1)3-y3=(x-1-y)[(x-1)2+(x-1)y+y2]
=(x-y-1)(x2+y2+xy-2x-y+1)
7. xm+4+xm+3-x-1=xm+3(x+1)-(x+1)=(x+1)(xm+3-1)
(Đúng nhớ like nhá !)
Minh Hải,Lê Thiên Anh,Nguyễn Huy Tú,Ace Legona,...giúp mk vs mai mk đi hk rùi

Ap dung bdt \(\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right).\left(x,y>0\right)\) lien tiep la duoc
Chuc bn thanh cong
svác-xơ ngược dấu.
\(\frac{16}{2a+3b+3c}=\frac{16}{\left(a+b\right)+\left(c+b\right)+\left(b+c\right)+\left(a+c\right)}\le\frac{1}{a+b}+\frac{2}{c+b}+\frac{1}{c+a}\)
Tương tự
\(\frac{16}{2b+3c+3a}\le\frac{1}{a+b}+\frac{1}{b+c}+\frac{2}{c+a}\)
\(\frac{16}{2c+3a+3b}\le\frac{2}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\)
Cộng lại ta được:
\(16VT\le4\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\)
\(\Rightarrow VT\le\frac{1}{4}\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\left(đpcm\right)\)

a,x^4+2x^3-4x-4
=(x^3+2x^3)-(4x+4)
=x^3(x+2)-4(x+2)
=(x^3-4)(x+2)
\(X^4+2X^3-4X-4\)
\(=\left(X^2\right)^2+2X^3-4X-2^2\)
\(=\left[\left(X^2\right)^2-2^2\right]+\left[2X^3-4X\right]\)
\(=\left(X^2+2\right)\left(X^2-2\right)+2X\left(X^2-2\right)\)
\(=\left(X^2-2\right)\left(X^2+2+2X\right)\)

a) a2−b2−4a+4
=(a2-4a+4)-b2
=(a-2)2-b2
=(a-2-b)(a-2+b)a2−b2−4a+4
b) x2+2x−3
=x2-x+3x-3
=x(x-1)+3(x-1)
=(x+3)(x-1)x2+2x−3
c) 4x2y2−(x2+y2)2
=(2xy-x2-y2)(2xy+x2+y2)
=-(x-y)2(x+y)2
d) 2a3−54b3
=2(a3-27b3)
=2(a-3b)(a2+3ab+9b2)

=a, a(b2+c2)+b(a2+c2)+c(a2+b2)+2abc
= ab2+ac2+ba2+bc2+ca2+cb2+2abc
= c2(a+b)+ab(a+b)+c(a2+b2+2ab)
= c2(a+b)+ab(a+b)+c(a+b)2
= (a+b)\(\left[c^2+ab+c\left(a+b\right)\right]\)
= (a+b)(c2+ab+ca+cb)
= (a+b)\(\left[c\left(a+c\right)+b\left(a+c\right)\right]\)
=(a+b)(a+c)(b+c)
b, a(b-c)3+b(c-a)3+c(a-b)3
= a(b-c)3-b\(\left[\left(b-c\right)+\left(a-b\right)\right]\)3+c(a-b)3
= a(b-c)3-b(b-c)3-3b(b-c)2(a-b)-3b(b-c)(a-b)2-b(a-b)3+c(a-b)3
= a(b-c)3-b(b-c)3-3b(b-c)(a-b)(b-c+a-b)-b(a-b)3+c(a-b)3
= a(b-c)3-b(b-c)3-3b(b-c)(a-b)(a-c)-b(a-b)3+c(a-b)3
= (b-c)3(a-b)-3b(b-c)(a-b)(a-c)-(a-b)3(b-c)
= (b-c)(a-b)\(\left[\left(b-c\right)^2-3b\left(a-c\right)-\left(a-b\right)^2\right]\)
=(b-c)(a-b)(b2-2bc+c2-3ab+3bc-a2+2ab-b2)
= (b-c)(a-b)(c2-a2+bc-ab)
= (b-c)(a-b)\(\left[\left(c-a\right)\left(c+a\right)+b\left(c-a\right)\right]\)
= (b-c)(a-b)(c-a)(c+a+b)
c, a2b2(a-b)+b2c2(b-c)+c2a2(c-a)
= a2b2(a-b)-b2c2\(\left[\left(a-b\right)+\left(c-a\right)\right]\)+c2a2(c-a)
= a2b2(a-b)-b2c2(a-b)-b2c2(c-a)+c2a2(c-a)
= b2(a-b)(a2-c2)+c2(c-a)(a2-b2)
= b2(a-b)(a-c)(a+c)-c2(a-c)(a-b)(a+b)
= (a-c)(a-b)\(\left[b^2\left(a+c\right)-c^2\left(a+b\right)\right]\)
= (a-c)(a-b)(b2a+b2c-c2a-c2b)
= (a-c)(a-b)\(\left[a\left(b^2-c^2\right)+bc\left(b-c\right)\right]\)
= (a-c)(a-b)\(\left[a\left(b-c\right)\left(b+c\right)+bc\left(b-c\right)\right]\)
= (a-c)(a-b)(b-c)\(\left[a\left(b+c\right)+bc\right]\)
= (a-c)(a-b)(b-c)(ab+ac+bc)
d, a4(b-c)+b4(c-a)+c4(a-b)
= a4(b-c)-b4[(b-c)+(a-b)]+c4(a-b)
= (b-c)(a4-b4)+(a-b)(c4-b4)
= (b-c)(a2-b2)(a2+b2)+(a-b)(c2-b2)(c2+b2)
= (b-c)(a-b)(a+b)(a^2+b^2)-(a-b)(b-c)(b+c)(b2+c2)
= (b-c)(a-b)(a3+ab2+ba2+b3-bc2-b3-cb2-c3)
= (b-c)(a-b)(a3+ab2+ba2-bc2-c3-cb2)
= (b-c)(a-b)(a3-c3)+b2(a-c)+b(a2-c2)
= (b-c)(a-b)(a-c)(a2+ac+c2)+b2(a-c)+b(a-c)(a+c)
= (b-c)(a-b)(a-c)(a2+ac+c2+b2+ab+ac)
= (a-b)(b-c)(c-a)(a2+b2+c2+ab+bc+ca)

Áp dụng Cauchy, ta có:
\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^2b\)
\(\Rightarrow\frac{1}{a^4+b^2+2ab^2}\le\frac{1}{2a^2b+2ab^2}\)
Tượng tự:
\(\frac{1}{b^4+a^2+2a^2b}\le\frac{1}{2a^2b+2ab^2}\)
\(\Rightarrow A\le\frac{2}{2ab\left(a+b\right)}\)
Lại có: \(\frac{1}{a}+\frac{1}{b}=2\)\(\Leftrightarrow\frac{a+b}{ab}=2\Rightarrow a+b=2ab\)
\(\Rightarrow A\le\frac{2}{\left(a+b\right)^2}\)
Áp dụng Schwarzt: \(2=\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\ge a+b\ge2\Rightarrow\left(a+b\right)^2\ge4\)
\(\Rightarrow A\le\frac{2}{4}=\frac{1}{2}\)
Dấu = xảy ra khi a=b=1
Áp dụng bđt cosi ta có :
A < = 1/2a^2b+2/ab^2 + 1/2ab^2+2a^2b
= 1/2ab . (1/a+b + 1/a+b) = 1/2ab . 2/a+b = 1/(a+b).(ab)
< = 1/\(\sqrt{ab}.2.ab\) = 1/2\(\sqrt{ab}^3\)
Có : 2 = 1/a + 1/b >= 2\(\sqrt{\frac{1}{ab}}\)
=> \(\sqrt{\frac{1}{ab}}\)< = 1
=> 1/ab < = 1
=> ab > =1
=> A < = 1/2.1 = 1/2
Dấu "=" xảy ra <=> a=b=1
Vậy GTLN của A = 1/2 <=> a=b=1
Tk mk nha
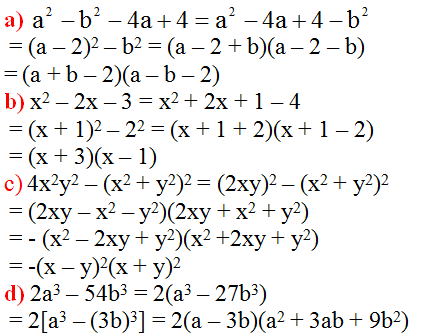
Lời giải:
$B=(a^4+b^4-2a^2b^2)+c^4-2c^2(a^2-b^2)-4b^2c^2$
$=(a^2-b^2)^2+c^4-2c^2(a^2-b^2)-(2bc)^2$
$=(a^2-b^2-c^2)^2-(2bc)^2$
$=(a^2-b^2-c^2-2bc)(a^2-b^2-c^2+2bc)$
$=[a^2-(b+c)^2][a^2-(b-c)^2]$
$=(a-b-c)(a+b+c)(a-b+c)(a+b-c)$