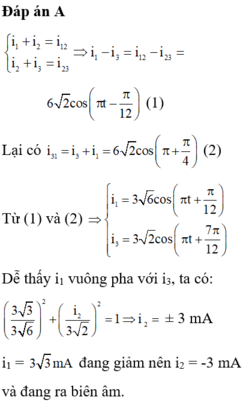
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
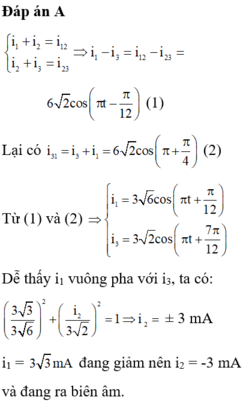
Sử sụng hệ thức: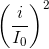 
+
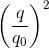= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =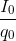 
= 50 (rad/s)
\(Z_L=100\Omega\)
\(Z_C=40\Omega\)
Theo giả thiết ta có:
\(R_1.R_2=(Z_L-Z_C)^2=60^2\)
\(R_1+R_2=\dfrac{U^2}{P}\)
\(\tan\varphi_1=\dfrac{60}{R_1}\)
\(\tan\varphi_2=\dfrac{60}{R_2}\)
Có: \(\varphi_1=2.\varphi_2\Rightarrow \tan \varphi_1=\tan 2\varphi_2=\dfrac{2\tan\varphi_2}{1-\tan^2\varphi_2}=\dfrac{60}{R_1}\)
\(\Rightarrow \dfrac{2\dfrac{60}{R_2}}{1-(\dfrac{60}{R_2})^2}=\dfrac{60}{R_1}\)
Biến đổi ta tìm đc \(R_2=60\sqrt 3\); \(R_1=20\sqrt 3\)
\(\Rightarrow P=\dfrac{U^2}{R_1+R_2}=60\sqrt 3(W)\)
Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)
