Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(-\frac{3}{6}=\frac{x}{-2}=-\frac{18}{y}=-\frac{z}{24}\)
Ta có :+) \(-\frac{3}{6}=\frac{x}{-2}\)
\(\Rightarrow x=\frac{\left(-3\right)\left(-2\right)}{6}\)
\(\Rightarrow x=1\)
+)\(-\frac{3}{6}=-\frac{18}{y}\)
\(\Rightarrow y=\frac{6.\left(-18\right)}{-3}\)
\(\Rightarrow y=36\)
+)\(-\frac{3}{6}=-\frac{z}{24}\)
\(\Rightarrow-z=\frac{\left(-3\right)24}{6}\)
\(\Rightarrow-z=-12\)
\(\Rightarrow z=12\)
Vậy........................

a) \(\frac{2.7.13}{26.35}=\frac{2.7.13}{2.13.5.7}=\frac{1}{5}\)
b) \(\frac{23.5-23}{4-27}=\frac{23.\left(5-1\right)}{-23}=\frac{23.4}{-23}=\frac{23.\left(-4\right)}{23}=-4\)
c) \(\frac{2130-15}{3550-25}=\frac{142.15-15}{142.25-25}=\frac{15.\left(142-1\right)}{25.\left(142-1\right)}=\frac{15.141}{25.141}=\frac{15}{25}=\frac{3.5}{5.5}=\frac{3}{5}\)
d) \(\frac{1717-101}{2828+404}=\frac{17.101-101}{28.101+101.4}=\frac{101.\left(17-1\right)}{101.\left(28+4\right)}=\frac{101.16}{101.32}=\frac{16}{32}=\frac{4.4}{2.4.4}=\frac{1}{2}\)
e) \(\frac{3.5.11.13}{33.35.27}=\frac{3.5.11.13}{3.11.5.7.3^3}=\frac{13}{7.3^3}=\frac{13}{189}\)
f) \(\frac{85-17+34}{51-102}=\frac{5.17-17+2.17}{3.17-6.17}=\frac{17.\left(5-1+2\right)}{17.\left(3-6\right)}=\frac{17.6}{17.\left(-3\right)}=\frac{6}{-3}=-2\)

a) \(\frac{2.7.13}{26.35}=\frac{2.7.13}{2.13.7.5}=\frac{1}{5}\)
b) \(\frac{3.5.11.13}{33.35.37}=\frac{3.5.11.13}{3.11.7.5.37}=\frac{13}{259}\)
c) \(\frac{23.5-23}{4-27}=\frac{23.\left(5-1\right)}{-23}=\frac{4}{-1}=-4\)
d) \(\frac{1717-101}{2828+404}=\frac{101.17-101}{404.7+404}=\frac{101.\left(17-1\right)}{404.\left(7+1\right)}=\frac{101.16}{404.8}=\frac{101.2.8}{101.4.8}=\frac{1}{2}\)

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

Rút gọn các phân số sau:
a, \(\dfrac{-315}{540}\) = \(\dfrac{-315:45}{540:45}\) = \(\dfrac{-7}{12}\)
b, \(\dfrac{25.13}{26.35}\) = \(\dfrac{5.5.13}{13.2.5.7}\) = \(\dfrac{5}{2.7}\) = \(\dfrac{5}{14}\)
c, \(\dfrac{3.13-13.18}{15.40-80}\) = \(\dfrac{3.13-13.18}{15.40-2.40}\) = \(\dfrac{13.\left(3-18\right)}{40.\left(15-2\right)}\)
= \(\dfrac{13.\left(-15\right)}{40.13}\) = \(\dfrac{-3}{8}\)
a) \(\dfrac{-315}{540}=\dfrac{-315:45}{540:45}=\dfrac{-7}{12}\)
b) \(\dfrac{25\cdot13}{26\cdot35}=\dfrac{5\cdot5\cdot13}{2\cdot13\cdot5\cdot7}=\dfrac{5}{2\cdot7}=\dfrac{5}{14}\)
c) \(\dfrac{3\cdot13-13\cdot18}{15\cdot40-80}=\dfrac{3\cdot13-13\cdot18}{15\cdot40-2\cdot40}=\dfrac{13\cdot\left(3-18\right)}{40\left(15-2\right)}=\dfrac{13\cdot\left(-15\right)}{40\cdot13}=\dfrac{1\cdot\left(-3\right)}{8\cdot1}=\dfrac{-3}{8}\)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)
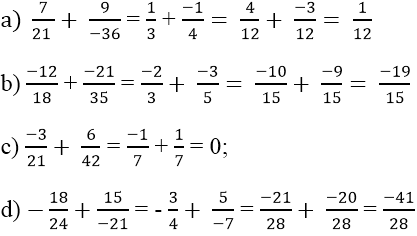
B2:
a) \(\dfrac{2.7.13}{26.35}=\dfrac{2.7.13}{2.13.7.5}=\dfrac{1}{5}\)
b) \(\dfrac{23.5-23}{4.27}=\dfrac{23.4}{4.27}=\dfrac{23}{27}\)
Phùng Tuệ Minh mk nghĩ câu c thế này :
c) \(\dfrac{85-17+34}{51-102}=\dfrac{34+51-17+34}{51-17+85}\)
\(=\dfrac{34+51-17+34}{51-17+34+51}\)
\(=\dfrac{34}{51}\)