Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện trở tương đương của mạch là
Rtd=R1+R2=48(ôm)
Điện trở tương đương sau khi mắc thêm R3 là
Rtd'=24/0,6=40(ôm)
Ta có (R1.R3)/(R1+R3)+R2=40
Hay (12.R3)/(12+R3)+36=40
=>R3=6(ôm)
Đoạn mạch A,B gồm 2 điện trở R1=12 ôm và R2=36 ôm mắc nối tiếp. Đặt 1 hdt không đổi 24V giữa 2 đầu đoạn mạch A,B
a) Tính điện trở tương đương của đoạn mạch A,B và hđt qua mỗi điện trở
b) Mắc thêm điện trở R3 song song với R1. Tính điện trở R3 để cđdđ qua đoạn mạch là 0.6A
Trả lời :
Điện trở tương đương của mạch là :
Rtd = R1 + R2 = 48 (ôm)
Điện trở td sau khi mắc thêm R3 là :
Rtd' = \(\dfrac{24}{0,6}=40\left(ôm\right)\)
Có :
\(\dfrac{\left(R1.R3\right)}{\left(R1+R3\right)+R2}=40\) hay \(\dfrac{\left(12.R3\right)}{\left(12+R3\right)+36}=40\)
=> R3=6 (ôm)

đặt R3=x(ôm)
\(=>P3=I3^2.x=\dfrac{U^2}{R23^2}.x=\dfrac{12^2x}{\left(8+x\right)^2}=\dfrac{12^2}{\left(\dfrac{8+x}{\sqrt{x}}\right)^2}=\dfrac{12^2}{\left(\dfrac{8}{\sqrt{x}}+\sqrt{x}\right)^2}\)
BDT AM-GM \(=>\left(\dfrac{8}{\sqrt{x}}+\sqrt{x}\right)^2\ge\left(2\sqrt{8}\right)^2=32=>P3\le\dfrac{12^2}{32}=4,5W\)
dấu"=" xảy ra<=>\(x=R3=8\left(om\right)\)

\(R1ntR2\Rightarrow P2=U2.I2=I2^2R2=Im^2.R2\)
\(\Rightarrow P2=\left(\dfrac{Um}{Rtd}\right)^2.R2=\left(\dfrac{12}{R1+R2}\right)^2.R2\)
\(\Rightarrow P2=\dfrac{12^2.R2}{\left(R1+R2\right)^2}=\dfrac{144R2}{\left(6+R2\right)^2}=\dfrac{144}{\dfrac{\left(6+R2\right)^2}{\sqrt{R2}^2}}=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\)
\(\Rightarrow\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2\ge\left(2\sqrt{6}\right)^2\ge24\left(AM-GM\right)\)
\(\Rightarrow P2=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\le\dfrac{144}{24}\le6W\Rightarrow P2max=6W\)
\(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow\dfrac{6}{\sqrt{R2}}=\sqrt{R2}\Leftrightarrow R2=6\Omega\)
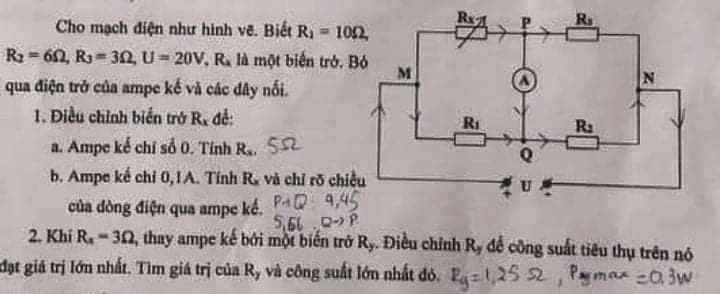
ta có : R4nt(R12//R3)
\(\Rightarrow R_{tđ}=R_4+R_{123}=R_4+\frac{R_{12}.R_3}{R_{12}+R_3}=0,8+\frac{\left(1+2\right).2}{\left(1+2\right)+2}=2\Omega\)
\(\Rightarrow\)I=\(\frac{U}{R_{tđ}}=\frac{6}{2}=3A\)
\(\Rightarrow\)I=I123=3A=I4
\(\Rightarrow U_4=R_4.I_4=0,8.3=2,4V\)
Có : R12//R3\(\Rightarrow\)R123=\(\frac{R_{12}.R_3}{R_{12}+R_3}=1,2\Omega\)
\(\Rightarrow\)U123=I123.R123=3.1,2=3,6V
\(\Rightarrow\)U12=U3=3,6V(R12//R3)
Có : I12=\(\frac{U_{12}}{R_{12}}=\frac{3,6}{3}=1,2A\)
\(\Rightarrow\)I1=I2=1,2A (R1nt R2)
\(\Rightarrow\)U1=I1.R1=1,2.1=1,2V
U2=I2.R2=1,2.2=2,4V