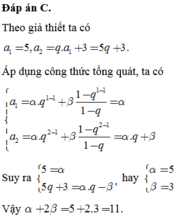C
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
Phạm Trần Hoàng Anh
CTVHS
20 tháng 8 2020
Cho dãy số : 2,6,10,14,...,2026.
a)Dãy số trên co bao nhiêu số hạng?
(2026 - 2) : 4 +1 = 507 SSH
b) Số 1014 có thuộc dãy số trên không? Vì sao?
thấy 2 : 4 dư 2
6 : 4 dư 2
10 : 4 dư2
.....
mà 1014 : 4 dư 2
=> 1014 là số thuộc dãy số trên
c) Tính tổng 10 số hạng đầu tiên của dãy số.
Thấy 2 : 4 = 0 dư 2
6 : 4 = 1 dư 2
.....
=> số hạng thứ 10 của dãy số trên là
9 x 4 + 2 = 38 ( do 0 -9 là 10 số )
=> tổng 10 số hạng đầu tiên là
10 . [38 + 2] : 2 = 200
25 tháng 3 2016
a) Giả sử các đỉnh đa giác là các điểm biểu diễn hình học các căn bậc n của đơn vị \(P_o=1\). Xét đa thức :
\(f=z^n-1=\left(z-1\right)\left(z-\omega\right)........\left(z-\omega^{n-1}\right),\omega=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n}\)
Rõ ràng :
\(n=f'\left(1\right)=\left(1-\omega\right)\left(1-\omega^2\right)...\left(1-\omega^{n-1}\right)\)
Lấy Modun 2 vế ta được kết quả
b) Ta có :
\(1-\omega^k=1-\cos\frac{2k\pi}{n}-i\sin\frac{2k\pi}{n}=2\sin^2\frac{k\pi}{n}-2i\sin\frac{k\pi}{n}\cos\frac{k\pi}{n}\)
\(=2\sin\frac{k\pi}{n}\left(\sin\frac{k\pi}{n}-i\cos\frac{k\pi}{n}\right)\)
Do đó : \(\left|1-\omega^k\right|=2\sin\frac{k\pi}{n},k=1,2,....,n-1\)
Sử dụng a) ta có điều phải chứng minh
c) Xét đa giác đều \(Q_oQ_1.....Q_{2n-1}\) nội tiếp trong đường tròn, các đỉnh của nó là điểm biểu diễn hình học của \(\sqrt{n}\) của đơn vị.
Theo a) \(Q_oQ_1.Q_oQ_2....Q_oQ_{2n-1}=2n\)
Bây giờ xét đa giác đều \(Q_oQ_2....Q_{2n-1}\) ta có \(Q_oQ_2.Q_oQ_4..Q_oQ_{2n-2}=n\)
Do đó \(Q_oQ_1.Q_oQ_3..Q_oQ_{2n-1}=2\) Tính toán tương tự phần b) ta được
\(Q_oQ_{2k-1}=2\sin\frac{\left(2k-1\right)\pi}{2n},k=1,2....n\) và ta có điều phải chứng minh