Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: \(P=\dfrac{x+\sqrt{x}+1+11\sqrt{x}-11+34}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+12\sqrt{x}+24}{\sqrt{x}+2}\)
b: Thay \(x=3-2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+12\left(\sqrt{2}-1\right)+24}{\sqrt{2}-1+2}\)
\(=\dfrac{27-2\sqrt{2}+12\sqrt{2}-12}{\sqrt{2}+1}=5+5\sqrt{2}\)
.
A= \(\left(\frac{a\sqrt{a}-1}{a-\sqrt{a}}-\frac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\frac{a+2}{a-2}\)
đkxđ: a>0 và a khác 1
A= \(\left[\frac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\frac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a+1}\right)}\right]:\frac{a+2}{a-2}\)
=\(\left(\frac{a+\sqrt{a}+1}{\sqrt{a}}-\frac{a-\sqrt{a}+1}{\sqrt{a}}\right).\frac{a-2}{a+2}\)
=\(\frac{2.\left(a-2\right)}{a+2}\)
A= \(2-\frac{8}{a+2}\)
muôn A nhỏ nhất thì a+2 nhỏ nhất mà a>0 và a khác 1
=> a=2
=> GTNN A=0 khi a=2
a) ĐKXĐ \(\Leftrightarrow\)\(\begin{cases}\sqrt{a}\ge0\\\sqrt{a}-1\ne0\\\sqrt{a}\ne0\\a-2\ne0\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a\ge0\\a\ne0\\a\ne1\\a\ne2\end{cases}\)\(\Leftrightarrow\begin{cases}a>0\\a\ne1\\a\ne2\end{cases}\)
b)\(A=\left[\frac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\frac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\right].\frac{a-2}{a+2}\)
\(=\left(\frac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}\right).\frac{a-2}{a+2}=\frac{2\sqrt{a}}{\sqrt{a}}\cdot\frac{a-2}{a+2}=\frac{2a-4}{a+2}\)
c)\(A=\frac{2a-4}{a+2}=\frac{2\left(a+2\right)-8}{a+2}=2-\frac{8}{a+2}\)
A đạt GTNN khi và chỉ khi \(\frac{8}{a+2}\) đạt GTLN khi và chỉ khi a+2 đạt giá trị nhỏ nhất
Mà min a+2 là 2 khi a=0 suy ra Min A\(=2-\frac{8}{2}=-2\)
Vậy Min A là -2 khi a=0
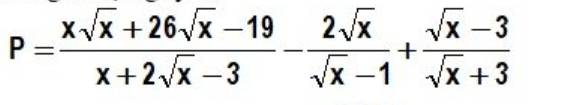
Lời giải:
a. ĐKXĐ: $x\geq 0; x\neq 1$
\(P=\frac{x\sqrt{x}+26\sqrt{x}-19}{(\sqrt{x}-1)(\sqrt{x}+3)}-\frac{2\sqrt{x}(\sqrt{x}+3)}{(\sqrt{x}-1)(\sqrt{x}+3)}+\frac{(\sqrt{x}-3)(\sqrt{x}-1)}{(\sqrt{x}+3)(\sqrt{x}-1)}\)
\(=\frac{x\sqrt{x}+26\sqrt{x}-19-(2x+6\sqrt{x})+(x-4\sqrt{x}+3)}{(\sqrt{x}+3)(\sqrt{x}-1)}\\ =\frac{x\sqrt{x}+16\sqrt{x}-x-16}{(\sqrt{x}+3)(\sqrt{x}-1)}\\ =\frac{(x+16)(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+3)}=\frac{x+16}{\sqrt{x}+3}\)
b.
$P=\frac{x+16}{\sqrt{x}+3}=\frac{(x-9)+25}{\sqrt{x}+3}$
$=(\sqrt{x}-3)+\frac{25}{\sqrt{x}+3}=(\sqrt{x}+3)+\frac{25}{\sqrt{x}+3}-6$
$\geq 2\sqrt{25}-6=4$ (áp dụng BĐT Cô-si)
Vậy $P_{\min}=4$. Giá trị này đạt tại $\sqrt{x}+3=\frac{25}{\sqrt{x}+3}\Leftrightarrow x=4$