Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
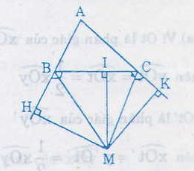
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc ˆBACBAC^
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)

Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của gócA

Hình bạn tự vẽ nha !
Chứng minh
a, Áp dụng định lí Pi-ta-go vào \(\Delta ABC\) vuông tại A , ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=8^2+6^2=64+36=100\)
\(\Rightarrow BC=10\)
b, Xét \(\Delta BEA\) và \(\Delta DEA\) có :
AB = AD (gt)
\(\widehat{BAE}=\widehat{DAE}\) (=1v)
AE chung
\(\Rightarrow\Delta BEA=\Delta DEA\left(c.g.c\right)\)
c, Xét \(\Delta BCD\) có CA là đường trung tuyến ứng với cạnh BD và \(EA=\dfrac{1}{3}AC\) nên E là trọng tâm của \(\Delta BCD\)
Vậy DE đi qua trung điểm của cạnh BC
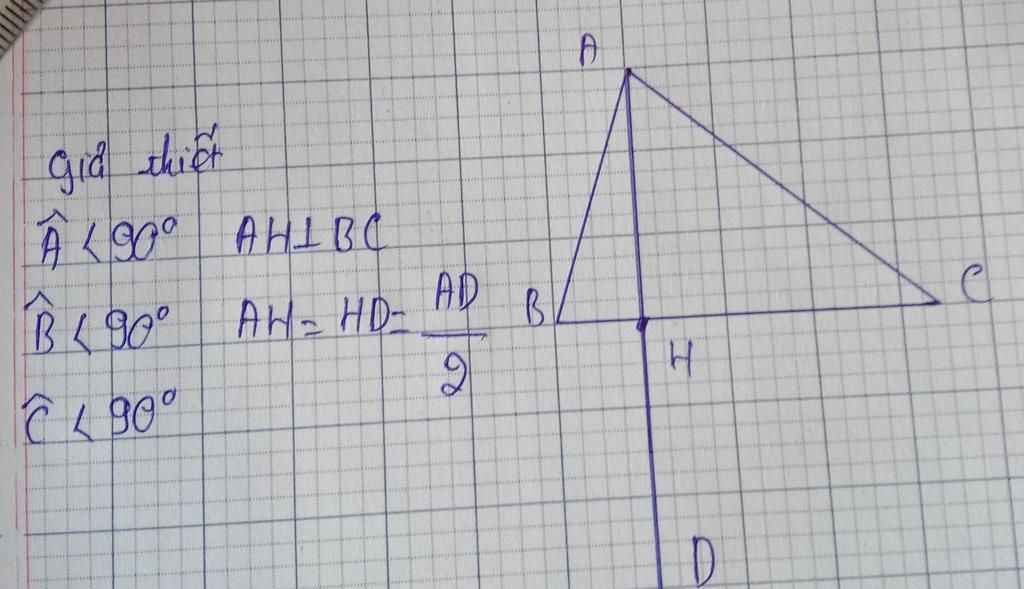






Xét ΔCHA vuông tại H và ΔCHD vuông tại H có
HC chung
HA=HD
Do đó: ΔCHA=ΔCHD
Suy ra: CA=CD