NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
LA
9 tháng 1 2024
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
NH
0
NT
6
17 tháng 10 2021
a) \(\left(2m-1\right)sinx+1-m=0\Rightarrow sinx=\dfrac{m-1}{2m-1}\)
Pt có nghiệm: \(-1\le\dfrac{m-1}{2m-1}\le1\)
\(\Rightarrow1-2m\le m-1\le2m-1\Rightarrow m\ge\dfrac{2}{3}\)
17 tháng 10 2021
b) \(\left(m+1\right)sin3x-cos3x=m+2\)
Pt có nghiệm: \(\left(m+1\right)^2+\left(-1\right)^2\ge\left(m+2\right)^2\)
\(\Rightarrow m^2+2m+1+1\ge m^2+4m+4\)
\(\Rightarrow-2m\ge2\Rightarrow m\le-1\)
HK
6 tháng 5 2021
hmm đóng góp ý kiến , lớp 11 giờ đã học đạo hàm rồi nhỉ , đạo hàm trên tử và mẫu đi xong thay giá trị =pi/3 vào là xong đáp án sẽ là -3 căn 3
DV
2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2022
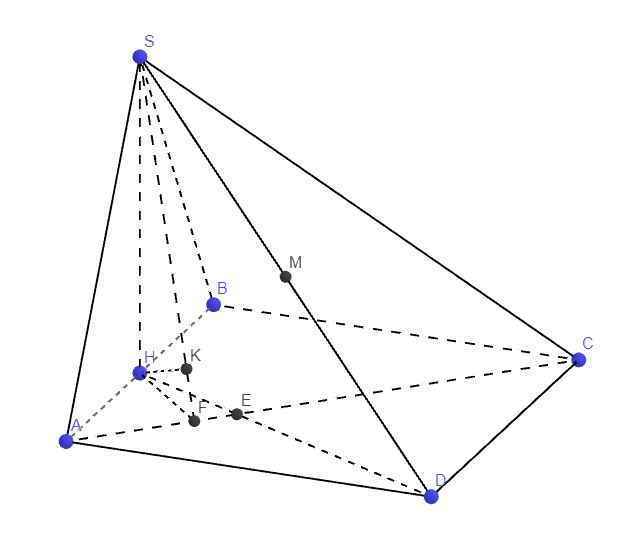
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)
Gọi M là trung điểm EG \(\Rightarrow AM\perp EG\) (tam giác cân)
\(\Rightarrow AM\perp\left(EFGH\right)\Rightarrow AM=d\left(A;\left(EFGH\right)\right)\)
\(EG=30-2x\Rightarrow EM=\dfrac{1}{2}EG=15-x\)
\(\Rightarrow AM=\sqrt{AE^2-EM^2}=\sqrt{x^2-\left(15-x\right)^2}=\sqrt{30x-225}\)
Do AEG là tam giác, theo BĐT tam giác: \(\left\{{}\begin{matrix}AE+AG>EG\\\left|AG-AE\right|< EG\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+x>30-2x\\0< 30-2x\end{matrix}\right.\) \(\Rightarrow\dfrac{15}{2}< x< 15\)
\(V=AD.S_{\Delta AEG}=30.\dfrac{1}{2}AM.EG=15.\left(30-2x\right)\sqrt{30x-225}\)
\(V^2=15^3.4\left(15-x\right)^2\left(2x-15\right)=15^3.4.\left(15-x\right)\left(15-x\right)\left(2x-15\right)\)
\(\le15^3.4.\left(\dfrac{15-x+15-x+2x-15}{3}\right)^3=...\)
Dấu "=" xảy ra khi \(15-x=2x-15\Rightarrow x=10\)
\(\Rightarrow d\left(A;\left(EFGH\right)\right)=AM=\sqrt{30.10-225}=5\sqrt{3}\)