Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
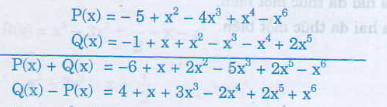 .
.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
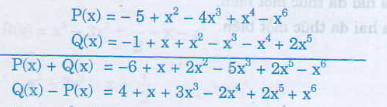

1) \(A\left(x\right)=-5x^3+3x^4+\frac{5}{7}-8x^2-10x\)
\(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)
\(B\left(x\right)=-2x^4-\frac{2}{7}+7x^2+8x^3+6x\)
\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)
2) \(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)
+
\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)
\(A\left(x\right)+B\left(x\right)=x^4+3x^3-x^2-4x+\frac{3}{7}\)
\(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)
-
\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)
\(A\left(x\right)-B\left(x\right)=5x^4-13x^3-15x^2-16x+1\)

a) \(A=\)\(x^4\)\(+4x^3\)\(+2x^2\)\(+x\)\(-7\)
\(B=\)\(2x^4\)\(-4x^3\)\(-2x^2\)\(-5x\)\(+3\)
b) f(x)= A(x)+B(x)= \(3x^4-4x\)\(-4\)
g(x)=A(x)-B(x) = \(-x^4+8x^3+4x^2+6x\)\(-10\)
c) g(x)= \(0^4+8.0^3+4.0^2\)\(+6.0\)\(-10\)
= -10
g(-2)=\(-2^4+8.-2^3+4.-2^2+6.-2\)\(-10\)
=\(-54\)

a) A(x) = \(x^2-5x^3+3x+\)\(2x^3\)= \(x^2+\left(-5x^3+2x^3\right)+3x\)=\(x^2-3x^3+3x\)
=\(-3x^3+x^2+3x\)
B(x)= \(-x^2+7+3x^3-x-5\)= \(-x^2+2+3x^3-x\)
=\(3x^3-x^2-x+2\)
b) A(x) - B(x) = \(-3x^3+x^2+3x\)- \(3x^3+x^2+x-2\)
=\(\left(-3x^3-3x^3\right)+\left(x^2+x^2\right)+\left(3x+x\right)-2\)= \(-6x^3+2x^2+4x-2\)
vậy A(x) - B(x) =\(-6x^3+2x^2+4x-2\)
c) C(x) = A(x) + B(x) =\(-3x^3+x^2+3x\)+ \(3x^3-x^2-x+2\)= 2x+2
ta có: C(x) = 0 <=> 2x+2=0
=> 2x=-2
=> x=-1
vậy x=-1 là nghiệm của đa thức C(x)
a) A(x)= -3x^3 + x^2 + 3x
B(x)= 3x^3 - x^2 - x +2
b) A(x) - B(x) = - 3x^3 + x^2 + 3x - (3x^3 - x^2 - x + 2)
= -3x^3 + x^2 + 3x - 3x^3 + x^2 + x - 2
= -6x^3 + 2x^2 + 4x -2
c) C(x) = A(x) + B(x) = - 3x^3 + x^2 + 3x + 3x^3 - x^2 - x +2= 2x + 2
C(x) có nghiệm => C(x)=0 => 2x + 2 = 0 => 2x=-2 => x=-1
Vậy x=-1 là nghiệm của C(x)

a) Thu gọn và sắp xếp:
M(x) = 2x4 – x4 + 5x3 – x3 – 4x3 + 3x2 – x2 + 1
= x4 + 2x2 +1
b)M(1) = 14 + 2.12 + 1 = 4
M(–1) = (–1)4 + 2(–1)2 + 1 = 4
Ta có M(x)=\(x^4+2x^2+1\)
Vì \(x^4\)và \(2x^2\)luôn lớn hơn hoặc bằng 0 với mọi x
Nên \(x^4+2x^2+1>0\)
Tức là M(x)\(\ne0\) với mọi x
Vậy đa thức trên không có nghiệm.
a) Sắp xếp các hạng tử của đa thức M(x) theo lũy thừa giảm của biến
M(x)=2x4−x4+5x3−x3−4x3+3x2−x2+1M(x)=2x4−x4+5x3−x3−4x3+3x2−x2+1
=x4+2x2+1=x4+2x2+1
b) M(1)=14+2.12+1=4M(1)=14+2.12+1=4
M(−1)=(−1)4+2.(−1)2+1=4

a) Thu gọn và sắp xếp đa thức trên theo lũy thừa tăng dần của biến
* \(P\left(x\right)=3x^5-5x^5+x^4-2x-x^5+3x^4-x^2+x+1\)
\(P\left(x\right)=1+\left(-2x+x\right)+\left(-x^2\right)+\left(x^4+3x^4\right)+\left(3x^5-5x^5-x^5\right)\)
\(P\left(x\right)=1-x-x^2+4x^4-3x^5\)
* \(Q_x=-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4\)
\(Q\left(x\right)=-5+\left(-2x+2x\right)+3x^2+\left(-3x^3\right)+\left(-3x^4\right)+\left(3x^5-x^5\right)\)
\(Q\left(x\right)=-5+3x^2-3x^3-3x^4+2x^5\)
b)
* \(P\left(x\right)+Q\left(x\right)=\left(3x^5-5x^2+x^4-2x-x^5+3x^4-x^2+x+1\right)+\left(-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4\right)\)
\(P\left(x\right)+Q\left(x\right)=\left(1-x-x^2+4x^4-3x^5\right)+\left(-5+3x^2-3x^3-3x^4+2x^5\right)\)\(P\left(x\right)+Q\left(x\right)=\left(1+-5\right)+\left(-x^2+3x^2\right)+\left(4x^4-3x^4\right)+\left(-3x^5+2x^5\right)-x-3x^3\)
\(P\left(x\right)+Q\left(x\right)=-4-x+x^2-3x^3+x^4-x^5\)
* \(P\left(x\right)-Q\left(x\right)=\left(3x^5-5x^2+x^4-2x-x^5+3x^4-x^2+x+1\right)-\left(-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4\right)\)
\(P\left(x\right)-Q\left(x\right)=\left(1-x-x^2+4x^4-3x^5\right)-\left(-5+3x^2-3x^3-3x^4+2x^5\right)\)
\(P\left(x\right)-Q\left(x\right)=1-x-x^2+4x^4-3x^5+5-3x^2+3x^3+3x^4-2x^5\)
\(P\left(x\right)-Q\left(x\right)=\left(1+5\right)+\left(-x^2-3x^2\right)+\left(4x^4+3x^4\right)+\left(-3x^5-2x^5\right)-x+3x^3\)
\(P\left(x\right)-Q\left(x\right)=6-4x+7x^4-5x^5-x+3x^3\)
\(A\left(x\right)=2x^3-3x^2+2x+1\)
\(B\left(x\right)=3x^3+2x^2-x+5\)
b) \(A\left(x\right)-B\left(x\right)=\left(2x^3-3x^2+2x+1\right)-\left(3x^3+2x^2-x+5\right)\)
\(A\left(x\right)-B\left(x\right)=2x^3-3x^3-3x^2-2x^2+2x+x+1-5\)
\(A\left(x\right)-B\left(x\right)=-x^3-5x^2+3x-4\)
a) A(x) = 2x3- 3x2 + 2x + 1
B(x) = 3x3 + 2x2 - x + 5
b) \(-\frac{2x^3-3x^2+2x+1}{3x^3+2x^2-x+5}\)= -x3 - 5x2 + 3x - 4