
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(4,=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}\right)^2-9}=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}=\dfrac{3\sqrt{3}-3\sqrt{2}+9}{2+\sqrt{6}}\\ =\dfrac{\left(3\sqrt{3}-3\sqrt{2}+9\right)\left(\sqrt{6}-2\right)}{2}\\ =\dfrac{9\sqrt{2}-6\sqrt{3}-6\sqrt{3}+6\sqrt{2}+9\sqrt{6}-18}{2}\\ =\dfrac{15\sqrt{2}-12\sqrt{3}+9\sqrt{6}-18}{2}\)
\(c,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=4\Leftrightarrow x-1=16\Leftrightarrow x=17\left(tm\right)\\ d,ĐK:x\ge-5\\ PT\Leftrightarrow\sqrt{x+5}=5\Leftrightarrow x+5=25\Leftrightarrow x=20\left(tm\right)\\ e,ĐK:x\ge0\\ PT\Leftrightarrow-2\sqrt{x}=-6\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ f,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)

Đặt \(\sqrt{x}=a\) . Khi đó , biểu thức trở thành :
\(\frac{1}{a^2+a}+\frac{2a}{a^2-1}-\frac{1}{a^2-a}\)= \(\frac{1}{a\left(a+1\right)}+\frac{2a}{\left(a-1\right)\left(a+1\right)}-\frac{1}{a\left(a-1\right)}\)
= \(\frac{a-1}{a\left(a-1\right)\left(a+1\right)}+\frac{2a.a}{\left(a-1\right)\left(a+1\right)a}-\frac{\left(a+1\right)}{a\left(a-1\right)\left(a+1\right)}\)
= \(\frac{a-1+2a^2-a-1}{a\left(a-1\right)\left(a+1\right)}\)= \(\frac{2a^2-2}{a\left(a-1\right)\left(a+1\right)}=\frac{2\left(a-1\right)\left(a+1\right)}{a\left(a-1\right)\left(a+1\right)}\)= \(\frac{2}{a}=\frac{2}{\sqrt{x}}\)
Điều kiện xác định bạn tự làm nhé



2:
a: =>x^2(5x^2+2)+2=0
x^2>=0
5x^2+2>=2
=>x^2(5x^2+2)>=0 với mọi x
=>x^2(5x^2+2)+2>=2>0 với mọi x
=>PTVN
b: x^4-12x^2+24=0
=>x^4-12x^2+36-12=0
=>(x^2-6)^2-12=0
=>(x^2-6-2căn 3)(x^2-6+2căn 3)=0
=>x^2=6+2căn 3 hoặc x^2=6-2căn 3
=>\(x=\pm\sqrt{6+2\sqrt{3}};x=\pm\sqrt{6-2\sqrt{3}}\)

1,\(\sqrt{\left(x-1\right)^2}=\left|x-1\right|=-\left(x-1\right)=1-x\)
2,\(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=-\left(a-2b\right)=2b-a\)
3,\(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)

Đặt \(\hept{\begin{cases}\sqrt[3]{x-16}=a\\\sqrt[3]{x+13}=b\end{cases}}\)
\(\Rightarrow b^3-a^3=29\)
Từ đó ta có hệ \(\hept{\begin{cases}1+a=b\\b^3-a^3=29\end{cases}}\)
Thế pt đầu vào pt sau ta được
\(a^3+3a^2+3a+1-a^3=29\)
\(\Leftrightarrow3a^2+3a-28=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=\frac{-3+\sqrt{345}}{6}\\a=\frac{-3-\sqrt{345}}{6}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}b=\frac{3+\sqrt{345}}{6}\\b=\frac{3-\sqrt{345}}{6}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{31\sqrt{345}+27}{18}\\x=\frac{-31\sqrt{345}+27}{18}\end{cases}}\)


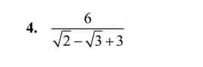
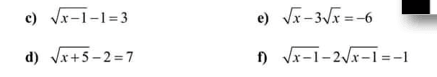



 Ai giúp mk vs ạ 🥲😞
Ai giúp mk vs ạ 🥲😞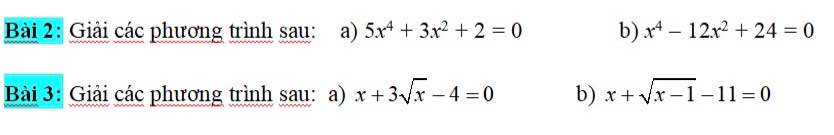

Cho tgiac ABC.A=90,dg cao AH.Gọi D và E lần lượt là điểm đối xứng của H qua AB,AC.CM
DE^2=4BD.CE