
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A=30+31+32+.......+32009
2A=31+32+............+32010
2A-A=(31+32+..........+32010)-(30+31+........+32009)
A=32010-30
A=32010-1
Cứ 1 nhóm có 4 số(3x3x3x3)=1
2010:4=502(dư 2)
Vì còn dư 2 =>3x3=9
Vậy tích trên có chữ số tận cùng là:
..........9-1=.........8
Vậy A chia hết cho 8
đặt A như đề bài ta có kết quả như bn Dũng
A bằng \(3^{2010}-1\)
Ta có \(3^{2010}\)bằng \(9^{1005}\)
Mà \(9\)đồng dư vs \(1\)(mod 8)
\(\Rightarrow9^{1005}\)đồng dư vs \(1^{1005}\)(mod 8)
\(\Rightarrow9^{1005}\)đồng dư vs \(1\)(mod 8)
\(\Rightarrow9^{1005}-1\)đồng dư vs \(0\)(mod 8)
Vậy A chia hết cho 8

ab/2 = 2(a + b + c)
ab/4 = a + b + c
(ab/4 - a - b)2 = c2
Theo Pytago ta có a2 + b2 = c2.
Suy ra (ab/4 - a - b)2 = a2 + b2
a2b2/16 + a2 + b2 + 2ab - a2b/2 - ab2/2 = a2 + b2
a2b2/16 - a2b/2 - ab2/2 + 2ab = 0
ab(ab/16 - a/2 - b/2 + 2) = 0
Vì ab ≠ 0 nên ta có ab - 8a - 8b + 32 = 0.
Hay ab - 8a - 8b + 64 - 32 = 0
a (b - 8) - 8(b - 8) = 32
(a - 8)(b - 8) = 32 = 1 x 32 = 8 x 4 = 2 x 16.
Các cặp (a - 8; b - 8) tương ứng là (1; 32), (8; 4), (2; 16).
Suy ra các cặp (a; b) tương ứng là (9; 40), (16; 12) và (10; 24). Từ đó suy ra c tương ứng trong các trường hợp lần lượt là 41; 20 và 26.
Vậy, các trường hợp của tam giác vuông có cạnh (a; b; c) thỏa mãn đề bài là
(9; 40; 41); (16; 12; 20) và (10; 24; 26).
Vì diện tích tam giác bằng 2 lần chu vi ta có :
\(\frac{ab}{2}=2\left(a+b+c\right)\)
\(\frac{ab}{4}=a+b+c\)
\(\left(\frac{ab}{4}-a-b\right)^2=c^2\)
Theo đeịnh lý PITAGO :
\(a^2+b^2=c^2\)\(\Rightarrow\)\(\left(\frac{ab}{4}-a-b\right)^2=a^2+b^2\)
\(\frac{a^2b^2}{16}+a^2+b^2+2ab-\frac{a^2b}{2}-\frac{ab^2}{2}=a^2+b^2\)
\(\frac{a^2b^2}{16}-\frac{a^2b}{2}+2ab=0\)
\(ab\left(\frac{ab}{16}-\frac{a}{2}-\frac{b}{2}+2\right)=0\)
Hay \(ab-8a-8b+32=0\)
\(a\left(b-8\right)-8\left(b-8\right)=32\)
\(\left(a-8\right)\left(b+8\right)=32=32.1=8.4=16.2\)
Các cặp ( a - 8 ; b - 8 ) tương ứng là ( 1 ; 32 ) ; ( 8 ; 4 ) ; ( 2 ; 16 )
Suy ra các cặp ( a ; b ) tương ứng là ( 9 ; 14 ) ; ( 16 ; 12 ) ; ( 10 ; 24 ) . Suy ra c tương ứng trong các trường hợp là 41 ; 20 và 26
Vậy các trường hợp của tam giác vuông có cạnh ( a ; b ; c ) thỏa mãn đề bài là ( 9 ; 40 ; 41 ) ; ( 16 ; 12 ; 20 ) ; ( 10 ; 24 ; 26 )

Cold Wind:nhưng mỗi lần kéo chuột lên nhìn đầu bài lại kéo xuống làm khó chiụ lắm
Nhiều quá bạn ơi ! Bạn nên chọn lọc những bài khó rồi đưa lên, chứ như vậy thì làm mấy ngày mới xong. Mình đoán đây là bài tập hè của bạn nhưng bạn lười làm nên lên đây hỏi

a/b=c/d =>a/c=b/d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)\(\Leftrightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left(\frac{a+b}{b+d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
\(\Rightarrow dpcm\)





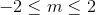 B.
B. 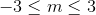
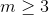











Đá án là : 16