K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 8 2017
bạn tự vẽ hình nha mk vẽ rùi mà lâu quá nên mk xóa lun
a) Cm tam giác DEC đd vs BAC
tam giác DEC và tam giác BAC có
C : góc chung
EDC = ABC =90 độ
=> tam giác DEC đd vs tam giác BAC (g-g)
b) Cm AEC đd với BDC
từ câu a => \(\frac{EC}{DC}=\frac{AC}{BC}\) ( 1)
Lại có C : góc chung (2)
Nên từ (1) và (2) => tam giác DEC đồng dạng với tam giác BDC ( c-g)
c) mk nghĩ đã
PH
0
LB
9 tháng 4 2020
Ta có:
\(\left(2x-1\right)^2+\left(x-2\right)\left(x+2\right)=\left(5x+1\right)\left(x-4\right)-12\)
\(\left(4x^2-4x+1\right)+x^2-4=5x^2-19x-4-12\)
\(5x^2-4x-3=5x^2-19x-16\)
\(\left(5x^2-5x^2\right)+\left(19x-4x\right)+\left(16-3\right)=0\)\(15x+13=0\)\(x=-\frac{13}{15}\)
18 tháng 4 2019
Câu 1 (2,0 điểm) Thực hiện phép tính:
a) 2xy.3x2y3
b) x.(x2 - 2x + 5)
c) (3x2 - 6x) : 3x
d) (x2 – 2x + 1) : (x – 1)
Câu 2 (2,0 điểm). Phân tích các đa thức sau thành nhân tử:
a) 5x2y - 10xy2
b) 3(x + 3) – x2 + 9
c) x2 – y2 + xz - yz
Câu 3 (2,0 điểm). Cho biểu thức: 
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?
b) Rút gọn biểu thức A.
c) Tìm giá trị của biểu thức A tại x = 1.
Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA.
Câu 5 (0,5 điểm). Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
Tk ủng hộ mk nha .
#Thiên_Hy
24 tháng 3 2022
-Lưu ý: Chỉ mang tính chất tóm tắt lại bài làm, bạn không nên trình bày theo!
c/ △ABC có: BD, CE là các đường cao và BD, CE cắt nhau tại H.
\(\Rightarrow\)AH là đường cao mà AH cắt BC tại Q \(\Rightarrow\)AH⊥BC tại Q.
△BEC∼△BQA (g-g) \(\Rightarrow\dfrac{BE}{BQ}=\dfrac{BC}{BA}\Rightarrow\dfrac{BE}{BC}=\dfrac{BQ}{BA}\)
\(\Rightarrow\)△BEQ∼△BCA (c-g-c) \(\Rightarrow\)\(\widehat{BQE}=\widehat{BAC}\) (1)
△BDC∼△AQC (g-g) \(\Rightarrow\dfrac{BC}{AC}=\dfrac{DC}{QC}\Rightarrow\dfrac{BC}{DC}=\dfrac{AC}{QC}\)
\(\Rightarrow\)△DQC∼△BCA (c-g-c) \(\Rightarrow\)\(\widehat{DQC}=\widehat{BAC}\) (2)
-Từ (1) và (2) suy ra: \(\widehat{BQE}=\widehat{DQC}\Rightarrow\widehat{AQE}=\widehat{AQD}\)
\(\Rightarrow\)QA là tia p/g của góc EQD
LH
3
23 tháng 5 2022
a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé
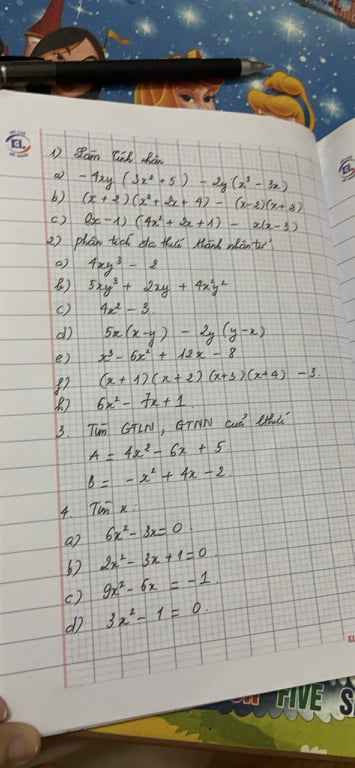
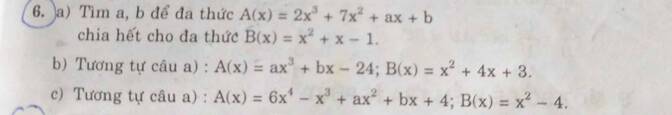
3. Tìm x biết
\(9x^2-4=0\)
\(\Rightarrow\left(3x\right)^2-2^2=0\)
\(\Rightarrow\left(3x-2\right).\left(3x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x-2=0\\3x+2=0\end{cases}}\Rightarrow\orbr{\begin{cases}3x=2\\3x=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=\frac{-2}{3}\end{cases}}\)
\(\left(3x+1\right)^2=\left(5x-2\right)^2\)
\(\Rightarrow\left(3x+1\right)^2-\left(5x-2\right)^2=0\)
\(\Rightarrow\left(3x+1-5x+2\right).\left(3x+1+5x-2\right)=0\)
\(\Rightarrow\left(-2x+3\right).\left(8x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}-2x+3=0\\8x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}-2x=-3\\8x=1\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=\frac{1}{8}\end{cases}}\)
\(4x^2-25+\left(2x+5\right).\left(2x+7\right)=0\)
\(\Rightarrow\left(4x^2-25\right)+\left(2x+5\right).\left(2x+7\right)=0\)
\(\Rightarrow\left(2x-5\right).\left(2x+5\right)+\left(2x+5\right).\left(2x+7\right)=0\)
\(\Rightarrow\left(2x+5\right).\left(2x-5+2x+7\right)=0\)
\(\Rightarrow\left(2x+5\right).\left(4x+2\right)=0\)
\(\Rightarrow2.\left(2x+5\right).\left(2x+1\right)=0\)
\(\Rightarrow\left(2x+5\right).\left(2x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x+5=0\\2x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}2x=-5\\2x=-1\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{-5}{2}\\x=\frac{-1}{2}\end{cases}}\)
\(x^3+4x^2+4x=0\)
\(\Rightarrow x.\left(x^2+4x+4\right)=0\)
\(\Rightarrow x.\left(x+2\right)^2=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\\left(x+2\right)^2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x+2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\)
\(x^2-10x+9=0\)
\(\Rightarrow x^2-x-9x+9=0\)
\(\Rightarrow x.\left(x-1\right)-9.\left(x-1\right)=0\)
\(\Rightarrow\left(x-9\right).\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-9=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=9\\x=1\end{cases}}\)
\(-3x^2+2x+1=0\)
\(\Rightarrow-3x^2+3x-x+1=0\)
\(\Rightarrow-3x.\left(x-1\right)-\left(x-1\right)=0\)
\(\Rightarrow\left(-3x-1\right).\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}-3x-1=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=1\end{cases}}\)
2. Phân tích đa thức sau thành nhân tử
\(x^4+64\)
\(=x^4+4x^3+8x^2-4x^3-16x^2-32x+8x^2-32x+64\)
\(=x^2.\left(x^2+4x+8\right)-4x.\left(x^2+4x+8\right)+8.\left(x^2+4x+8\right)\)
\(=\left(x^2-4x+8\right).\left(x^2+4x+8\right)\)
\(x^4-x^2+1\) (Bạn xem lại đề nhé.)