NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
Giúp em với, em đg cần thực sự gấp ạ!!!
2
19 tháng 8 2021
Bài 1:
a) \(\left(2x+y\right)^2-\left(y-2x\right)^2=\left(2x+y-y+2x\right)\left(2x+y+y-2x\right)=8xy\)
b) \(\left(x-y\right)^2+2\left(x^2-y^2\right)+\left(x+y\right)^2\\ =x^2-2xy+y^2+2x^2-2y^2+x^2+2xy+y^2\\ =4x^2\)
c) \(\left(x-2y\right)\left(x+2y\right)=x^2-4y^2\)
d) \(\left(y-\dfrac{1}{2}\right)\left(y+\dfrac{1}{2}\right)=y^2-\dfrac{1}{4}\)
20 tháng 8 2021
Bài 1:
a: \(\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=4x^2+4xy+y^2-y^2+4xy-4x^2\)
=8xy
b: Ta có: \(\left(x-y\right)^2+2\left(x^2-y^2\right)+\left(x+y\right)^2\)
\(=\left(x-y+x+y\right)^2\)
\(=\left(2x\right)^2\)
\(=4x^2\)
c: \(\left(x-2y\right)\left(x+2y\right)=x^2-4y^2\)
d: \(\left(y-\dfrac{1}{2}\right)\left(y+\dfrac{1}{2}\right)=y^2-\dfrac{1}{4}\)
29 tháng 5 2022
Mik cần lời giải á, các bạn toàn cho mik đáp án hoặc là cho mỗi câu 123 (Q▪︎Q)
29 tháng 10 2021
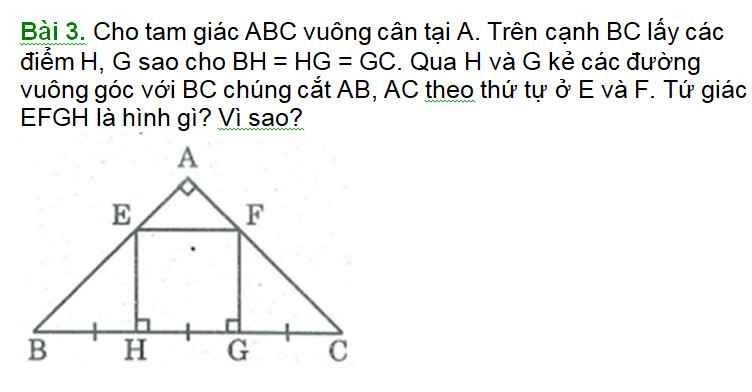
Xét tứ giác EHGF có:
EH//GF(cùng vuôn góc BC)
\(\widehat{EHG}=90^0\)(EH⊥HG)
=> EHGF là hình chữ nhật(1)
Xét tam giác EBG có:
EH là đường cao(EH⊥BG)
EH là trung tuyến(BH=HG)
=> Tam giác EBG cân tại E
Mà \(\widehat{EBH}=45^0\)(ABC vuông cân tại A)
=> Tam giác EBG vuông cân tại E
=> \(EH=\dfrac{1}{2}BG=HG\left(2\right)\)(EH là trung tuyến ứng với cạnh huyền)
\(\left(1\right),\left(2\right)\Rightarrow\) EHGF là hình vuông
15 tháng 11 2021
\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
NV
0
29 tháng 12 2023
\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3
HP
9 tháng 7 2016
\(Q=x^2+y^2+xy+x+y+10\)
\(=\left(x^2+xy+x\right)+y^2+y+10\)
\(=x^2+x\left(y+1\right)+y^2+y+10\)
\(=x^2+2.x.\frac{y+1}{2}+\left(\frac{y+1}{2}\right)^2+y^2+y-\left(\frac{y+1}{2}\right)^2+10\)
\(=\left(x+\frac{y+1}{2}\right)^2+y^2+y-\frac{\left(y+1\right)^2}{4}+10\)
\(=\left(x+\frac{y+1}{2}\right)^2+y^2+y-\frac{y^2+2y+1}{4}+10\)
\(=\left(x+\frac{y+1}{2}\right)^2+y^2+y-\frac{1}{4}y^2-\frac{1}{2}y-\frac{1}{4}+10\)
\(=\left(x+\frac{y+1}{2}\right)^2+\frac{3}{4}y^2+\frac{1}{2}y+\frac{39}{4}\)
\(=\left(x+\frac{y+1}{2}\right)^2+\frac{3}{4}\left(y^2+\frac{2}{3}y+13\right)=\left(x+\frac{y+1}{2}\right)^2+\frac{3}{4}\left(y^2+2.y.\frac{2}{6}+\frac{4}{36}-\frac{4}{36}+13\right)\)
\(=\left(x+\frac{y+1}{2}\right)^2+\frac{3}{4}\left[\left(y+\frac{2}{6}\right)^2+\frac{116}{9}\right]=\left(\frac{2x+y+1}{2}\right)^2+\frac{3}{4}\left(y+\frac{2}{6}\right)^2+\frac{29}{3}\)
Vì \(\left(\frac{2x+y+1}{2}\right)^2\ge0;\frac{3}{4}\left(y+\frac{2}{6}\right)^2\ge0=>\left(\frac{2x+y+1}{2}\right)^2+\frac{3}{4}\left(y+\frac{2}{6}\right)^2+\frac{29}{3}\ge\frac{29}{3}>0\) (với mọi x;y)
Vậy biểu thức Q luôn dương với mọi giá trị của biến
9 tháng 7 2016
=>4Q=4x2+4xy+4y2+4x+4y+40
=4x2+4x(y+1)+(y+1)2+4y2-y2+4y-2y+40-1
=(2x+y+1)2+3y2+2y+39
\(=\left(2x+y+1\right)^2+\left(\sqrt{3}y+\frac{\sqrt{3}}{3}\right)^2+\frac{116}{3}\)
\(\Rightarrow Q=\left(\frac{2x+y+1}{2}\right)^2+\left(\frac{\sqrt{3}y+\frac{\sqrt{3}}{3}}{2}\right)^2+\frac{29}{3}>0\)
=>đpcm
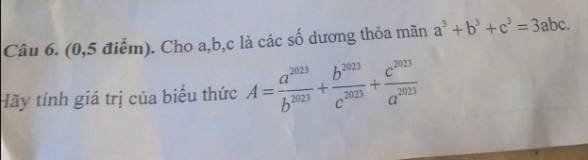
a: \(AO=\dfrac{1}{2}AC\)(O là trung điểm của AC)
nên AO=AD
hay ΔAOD cân tại A