
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 15:
\(P=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{x-y}{2xy}\cdot\dfrac{xy+y^2+xy-y^2}{x\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{x}\)


\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)

\(A=111.....111.10^{2017}+2222.....2222.10+5\)
\(=\frac{10^{2015}-1}{9}.10^{2017}+20.\frac{10^{2016}-1}{9}+5\)
\(=\frac{10^{4032}-10^{2017}+2.10^{2017}-20+45}{9}\)
\(=\frac{10^{4032}+2.5.10^{2016}+25}{9}\)
\(=\left(\frac{10^{2016}+5}{3}\right)^2\) là số chính phương (ĐPCM)
đề bài bảo có 2005 số 2 nên phải là 10^2006 chứ bạn, mấy cái còn lại cũng thế!


a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)


Sao lạ thế nhỉ, áp cái được luôn?
\(2a+\frac{b}{a}+\frac{c}{b}\ge3\sqrt[3]{2a.\frac{b}{a}.\frac{c}{b}}=3\sqrt[3]{2c}\)
Đẳng thức tự xét.
 cd
cd ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
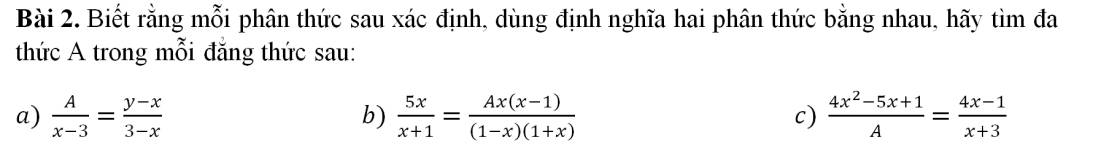 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 
\(abc=a+b+c\Leftrightarrow\frac{abc}{abc}=\frac{a+b+c}{abc}\)
\(\Leftrightarrow1=\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=Q\)
\(\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)\)
\(\Rightarrow P=3^2-2Q=9-2=7\)