Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.

Bạn có thể ghi rõ đạo hàm \(f'\left(x\right)\) không? Căn thức đến chỗ nào vậy?

Hàm số: \(f\left(x\right)=\frac{x^3}{3}-\frac{x^2}{2}-6x+\frac{3}{4}\)
A) Đồng biến trên khoảng (-2; 3)
B) Nghịch biến trên khoảng (-2; 3)
C) Nghịch biến trên khoảng (-∞; -2)
D) Đồng biến trên khoảng (-; +∞)

1.
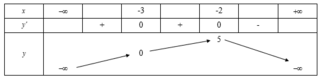
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
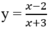
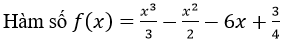

T
L câu hỏi là gì zậy bn :)
HT
7b/5 ) trong dod#$^&*())*&YYÚGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
thực ra tui ko biết đâu