LN
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
14 tháng 2 2017
Lời giải:
Sử dụng công thức phương trình tiếp tuyến tại \(x_0\) là:
\(y=f'(x_0)(x-x_0)+f(x_0)\)
Ta có phương trình hai đường thẳng là tiếp tuyến của đồ thị \(y=x^2-4x+5\) tại \(A,B\) là:\(\left\{\begin{matrix}y=-2x+4\\y=4x-11\end{matrix}\right.\)
Ta có: \(x^2-4x+5-(-2x+4)=x^2-2x+1=(x-1)^2=0\Leftrightarrow x=1\)
\(x^2-4x+5-(4x-11)=(x-4)^2=0\Leftrightarrow x=4\)
\((-2x+4)-(4x-11)=0\Leftrightarrow x=\frac{5}{2}\)
Do đó diện tích hình phẳng giới hạn bởi các đường đã cho là:
\(\int ^{4}_{\frac{5}{2}}|(x-4)^2|dx+\int ^{\frac{5}{2}}_{1}|(x-1)^2|dx=\frac{9}{8}+\frac{9}{8}=\frac{9}{4}\)
\(\Rightarrow a+b=9+4=13\)
ta được kết quả nào sau đây?
.
.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2019
\(z\ne4i\Rightarrow\left\{{}\begin{matrix}a\ne0\\b\ne4\end{matrix}\right.\)
\(\frac{z-4}{z-4i}=\frac{a-4+bi}{a+\left(b-4\right)i}=\frac{\left(a-4+bi\right)\left(a-\left(b-4\right)i\right)}{a^2-\left(b-4\right)^2}=\frac{a\left(a-4\right)+b\left(b-4\right)-\left[\left(a-4\right)\left(b-4\right)-ab\right]i}{a^2-\left(b-4\right)^2}\)
Số phức trên là thuần ảo khi và chỉ khi \(\left\{{}\begin{matrix}a\left(a-4\right)+b\left(b-4\right)=0\\\left(a-4\right)\left(b-4\right)-ab\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-2\right)^2=8\\a+b-4\ne0\end{matrix}\right.\)
\(\Rightarrow\) Tập hợp \(z\) là điểm \(M\left(a;b\right)\) thuộc đường tròn (C) tâm \(I\left(2;2\right)\) bán kính \(R=2\sqrt{2}\) và khác 2 điểm \(A\left(0;4\right)\) và \(B\left(4;0\right)\)
\(P=\left|z\right|^2=a^2+b^2=OM^2\)
\(P_{max}\) khi M trùng giao điểm của đường thẳng OI và đường tròn (giao điểm năm khác phía O so với I)
Phương trình OI: \(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
Giao điểm của OI và (C): \(2\left(x-2\right)^2=8\Rightarrow\left(x-2\right)^2=4\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)
\(\Rightarrow M_1\left(0;0\right)\) (loại); \(M_2\left(4;4\right)\) \(\Rightarrow a=b=4\)
Không có kết quả?!
PT
1
PT
1
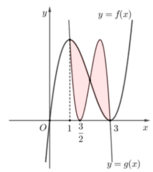
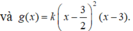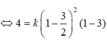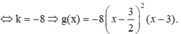
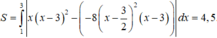
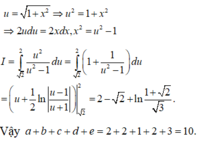
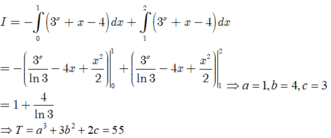
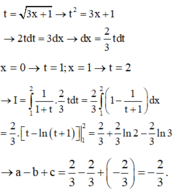
giả sử a = 1 ; b = 2 ; c = 3 ; d = 4 ; e = 5
a+b+c+d+e= 1 + 2 + 3 + 4 + 5 = 15
=abcde
nghĩ vậy