IS
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
2 tháng 1 2023
\(a,đk\left(B\right):x\ne\pm3\\ B=\dfrac{3}{x-3}-\dfrac{6x}{9-x^2}+\dfrac{x}{x+3}\\ =\dfrac{3}{x-3}+\dfrac{6x}{x^2-9}+\dfrac{x}{x+3}\\ =\dfrac{3\left(x+3\right)+6x+x\left(x-3\right)}{x^2-9}\\ =\dfrac{3x+9+6x+x^2-3x}{x^2-9}\\ =\dfrac{x^2+6x+9}{x^2-9}\\ =\dfrac{\left(x+3\right)^2}{x^2-9}\\ =\dfrac{x+3}{x-3}\)
\(b,P=A.B\\ =\dfrac{x+1}{x+3}\times\dfrac{x+3}{x-3}\\ =\dfrac{x+1}{x-3}\)
\(c,\) Để P nguyên
\(\dfrac{x+1}{x-3}=1+\dfrac{4}{x-3}\)
=> \(x-3\inƯ\left(4\right)\)
\(Ư\left(4\right)=\left\{-1;1;2;-2;4;-4\right\}\)
\(=>x=\left\{2;4;5;1;7;-1\right\}\)
14 tháng 12 2023
Câu 6:
ĐKXĐ: \(x\ne-\dfrac{1}{3}\)
Để \(\dfrac{9x+4}{3x+1}\in Z\) thì \(9x+4⋮3x+1\)
=>\(9x+3+1⋮3x+1\)
=>\(1⋮3x+1\)
=>\(3x+1\in\left\{1;-1\right\}\)
=>\(3x\in\left\{0;-2\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3}\right\}\)
mà x nguyên
nên x=0
Câu 2:
a: ĐKXĐ: \(x\notin\left\{2;-2;0\right\}\)
b: \(A=\left(\dfrac{1}{x+2}-\dfrac{2x}{4-x^2}+\dfrac{1}{x-2}\right)\cdot\dfrac{x^2-4x+4}{4x}\)
\(=\left(\dfrac{1}{x+2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x-2}\right)\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{x-2+2x+x+2}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{4x\left(x-2\right)}{4x\left(x+2\right)}=\dfrac{x-2}{x+2}\)
KT
10 tháng 1 2018
BÀI 1:
a) \(ĐKXĐ:\) \(x-3\)\(\ne\)\(0\)
\(\Leftrightarrow\)\(x\)\(\ne\)\(3\)
b) \(A=\frac{x^3-3x^2+4x-1}{x-3}\)
\(=\frac{\left(x^3-3x^2\right)+\left(4x-12\right)+11}{x-3}\)
\(=\frac{x^2\left(x-3\right)+4\left(x-3\right)+11}{x-3}\)
\(=x^2+4+\frac{11}{x-3}\)
Để \(A\)có giá trị nguyên thì \(\frac{11}{x-3}\)có giá trị nguyên
hay \(x-3\)\(\notinƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Ta lập bảng sau
\(x-3\) \(-11\) \(-1\) \(1\) \(11\)
\(x\) \(-8\) \(2\) \(4\) \(14\)
Vậy....
28 tháng 3 2018
a) Vì mỗi đơn thức là một đa thức nên ta có thể viết bất kỳ đơn thức nào ở câu này.
Ví dụ: P(x) = xy2 (Vì đơn thức cũng là một đa thức)
b) Có vô số đa thức không phải là đơn thức.
Ví dụ: 2x + 3y; x2 + 2y
4 tháng 1 2022
a: ĐKXĐ: \(x\notin\left\{5;-5\right\}\)
b: \(P=\dfrac{x-5+2x+10-2x-10}{\left(x+5\right)\left(x-5\right)}=\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}=\dfrac{1}{x+5}\)
CM
28 tháng 3 2018
a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.
Vậy điều kiện : x2 – 1 ≠ 0
x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1
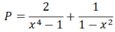
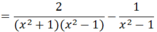
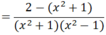
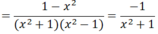
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1
29 tháng 10 2020
\(P=\frac{a+2}{a+3}-\frac{5}{\left(a+3\right)\left(a-2\right)}-\frac{a}{a^2-2a}\)
a) ĐKXĐ : \(\hept{\begin{cases}a\ne0\\a\ne-3\\a\ne2\end{cases}}\)
b)\(=\frac{a+2}{a+3}-\frac{5}{\left(a+3\right)\left(a-2\right)}-\frac{a}{a\left(a-2\right)}\)
\(=\frac{a\left(a-2\right)\left(a+2\right)}{a\left(a+3\right)\left(a-2\right)}-\frac{5a}{a\left(a+3\right)\left(a-2\right)}-\frac{a\left(a+3\right)}{a\left(a+3\right)\left(a-2\right)}\)
\(=\frac{a\left(a^2-4\right)}{a\left(a+3\right)\left(a-2\right)}-\frac{5a}{a\left(a+3\right)\left(a-2\right)}-\frac{a^2+3a}{a\left(a+3\right)\left(a-2\right)}\)
\(=\frac{a^3-4a-5a-a^2-3a}{a\left(a+3\right)\left(a-2\right)}\)
\(=\frac{a^3-a^2-12a}{a\left(a+3\right)\left(a-2\right)}=\frac{a\left(a^2-a-12\right)}{a\left(a+3\right)\left(a-2\right)}\)
\(=\frac{a^2-4a+3a-12}{\left(a+3\right)\left(a-2\right)}=\frac{a\left(a-4\right)+3\left(a-4\right)}{\left(a+3\right)\left(a-2\right)}\)
\(=\frac{\left(a-4\right)\left(a+3\right)}{\left(a+3\right)\left(a-2\right)}=\frac{a-4}{a-2}\)
c) \(8a=8a^2\)
⇔ \(8a^2-8a=0\)
⇔ \(8a\left(a-1\right)=0\)
⇔ \(\orbr{\begin{cases}8a=0\\a-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=0\left(ktm\right)\\a=1\left(tm\right)\end{cases}}\)
Với a = 1 =>\(P=\frac{1-4}{1-2}=\frac{-3}{-1}=3\)
4 tháng 1 2022
a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b: \(P=\dfrac{x}{2\left(x-1\right)}-\dfrac{x^2+1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+x-x^2-1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{2x+2}\)
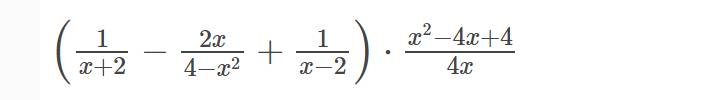
ĐKXĐ la B>=0 bn nhé