Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng các HĐT \(\left\{{}\begin{matrix}a^2+b^2=\left(a+b\right)^2-2ab\\a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\end{matrix}\right.\)
\(\left(sin^2x\right)^2+\left(cos^2x\right)^2-\left[\left(sin^2x\right)^3+\left(cos^2x\right)^3\right]\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x-\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]\)
\(=1-2sin^2x.cos^2x-1+3sin^2x.cos^2x\)
\(=sin^2x.cos^2x\)

\(y=\frac{\cos^4a+\sin^2a-\cos^2a}{\sin^4a+\cos^2a-\sin^2a}\)
\(\Leftrightarrow y=\frac{\cos^4a+\left(1-\cos^2a\right)-\cos^2a}{\left(\sin^2a\right)^2+\cos^2a-\sin^2a}\)
\(\Leftrightarrow y=\frac{\cos^4a+1-2\cos^2a}{\left(1-\cos^2a\right)^2+\cos^2a-\left(1-\cos^2a\right)}\)
\(\Leftrightarrow y=\frac{\left(1-\cos^2a\right)^2}{1-2\cos^2a+\cos^4a+2\cos^2a-1}\)
\(\Leftrightarrow y=\frac{\left(\sin^2a\right)^2}{\cos^4a}\)
\(\Leftrightarrow y=\frac{\sin^4a}{\cos^4a}\)
\(\Leftrightarrow y=\tan^4a\)
Vậy \(y=\tan^4a\)

cái câu 1 kia lạ thật, phần phía trc có ngoặc thì phải nhân vs hạng tử nào đó chứ nhỉ? Và mk tính ra kq là \(-\cos^22\alpha\)
\(VT=\cos^4\alpha+\sin^4\alpha-2\cos^6\alpha-2\sin^6\alpha\)
\(=\sin^4\alpha\left(1-2\sin^2\alpha\right)-\cos^4\alpha\left(2\cos^2\alpha-1\right)\)
\(=\sin^4\alpha.\cos2\alpha-\cos^4\alpha.\cos2\alpha\)
\(=\cos2\alpha\left(\sin^2\alpha.\sin^2\alpha-\cos^4\alpha\right)\)
\(=\cos2\alpha.\left[\left(1-\cos^2\alpha\right)^2-\cos^4\alpha\right]\)
\(=\cos2\alpha.\left(1-2\cos^2\alpha\right)\)
\(=-\cos^22\alpha\)
2/ \(VT=\frac{1-\cos^2\alpha+\cos^2\alpha}{1+\sin2\alpha}=\frac{1}{1+\sin2\alpha}\)
\(VP=\frac{\frac{\sin\alpha}{\cos\alpha}-1}{\frac{\sin\alpha}{\cos\alpha}+1}=\frac{\frac{\sin\alpha-\cos\alpha}{\cos\alpha}}{\frac{\sin\alpha+\cos\alpha}{\cos\alpha}}=\frac{\sin\alpha-\cos\alpha}{\sin\alpha+\cos\alpha}\)
hmm, câu 2 có vẻ vô lí, bn thử nhân chéo lên mà xem, nó ko ra KQ = nhau đâu
1)
\((\cos^4a+\sin ^4a)-2(\cos^6a+\sin ^6a)=(\cos ^4a+\sin ^4a)-2(\cos ^2a+\sin ^2a)(\cos ^4a-\cos ^2a\sin ^2a+\sin ^4a)\)
\(=(\cos ^4a+\sin ^4a)-2(\cos ^4a-\cos ^2a\sin ^2a+\sin ^4a)\)
\(=-(\cos ^4a-2\sin ^2a\cos ^2a+\sin ^4a)=-(\cos ^2a-\sin ^2a)^2=-\cos ^22a\)
(bạn xem lại đề. Nếu thay $(\cos ^4a+\sin ^4a)$ thành $3(\cos ^4a+\sin ^4a)$ thì kết quả thu được là $(\cos ^2a+\sin ^2a)^2=1$ như yêu cầu)
2) Sửa đề:
\(\frac{\sin ^2a-\cos ^2a}{1+2\sin a\cos a}=\frac{(\sin a-\cos a)(\sin a+\cos a)}{\sin ^2a+\cos ^2a+2\sin a\cos a}=\frac{(\sin a-\cos a)(\sin a+\cos a)}{(\sin a+\cos a)^2}\)
\(=\frac{\sin a-\cos a}{\sin a+\cos a}=\frac{\frac{\sin a}{\cos a}-1}{\frac{\sin a}{\cos a}+1}=\frac{\tan a-1}{\tan a+1}\)
Bạn lưu ý viết đề bài chuẩn hơn.

Đề bài không chính xác, biểu thức này vẫn phụ thuộc a
Đề bài đúng phải là: \(\sqrt{sin^4a+4cos^2a}+\sqrt{cos^4a+4sin^2a}\)

a/ \(VT=\frac{\sin^4x+2\sin x.\cos x-\left(1-\sin^2x\right)^2}{\frac{\sin2x}{\cos2x}-1}\)
\(=\frac{\sin^4x+2\sin x.\cos x-1+2\sin^2x-\sin^4x}{\frac{\sin2x-\cos2x}{\cos2x}}\) \(=\frac{1-2\sin^2x-\sin2x}{\frac{\cos2x-\sin2x}{\cos2x}}=\frac{\cos2x-\sin2x}{\frac{\cos2x-\sin2x}{\cos2x}}=\cos2x=VP\)

Lời giải:
a)
\(\frac{\sin ^2a+2\cos ^2a-1}{\cot ^2a}=\frac{(\sin ^2a+\cos ^2a)+\cos ^2a-1}{\cot ^2a}=\frac{1+\cos ^2a-1}{\cot ^2a}=\frac{\cos ^2a}{\cot ^2a}=\frac{\cos ^2a}{(\frac{\cos a}{\sin a})^2}=\sin ^2a\)
b)
\(\frac{1-\sin ^2a\cos ^2a}{\cos ^2a}-\cos ^2a=\frac{1}{\cos ^2a}-\sin ^2a-\cos ^2a\)
\(=\frac{\sin ^2a+\cos ^2a}{\cos ^2a}-(\sin ^2a+\cos ^2a)=\tan ^2a+1-1=\tan ^2a\)
c)
\(\frac{\sin ^2a-\tan ^2a}{\cos ^2a-\cot ^2a}=\frac{\sin ^2a-\frac{\sin ^2a}{\cos ^2a}}{\cos ^2a-\frac{\cos ^2a}{\sin ^2a}}=\frac{\sin ^4a(\cos ^2a-1)}{\cos ^4a(\sin ^2a-1)}\)
\(=\frac{\sin ^4a(-\sin ^2a)}{\cos ^4a(-\cos ^2a)}=\frac{\sin ^6a}{\cos ^6a}=\tan ^6a\)

\(\frac{cos\left(a-b\right)}{sin\left(a+b\right)}=\frac{cosa.cosb+sina.sinb}{sina.cosb+cosa.sinb}=\frac{\frac{cosa.cosb}{sina.sinb}+1}{\frac{sina.cosb}{sina.sinb}+\frac{cosa.sinb}{sina.sinb}}=\frac{cota.cotb+1}{cota+cotb}\)
Bạn ghi đề ko đúng
\(sin\left(a+b\right)sin\left(a-b\right)=\frac{1}{2}\left[cos2b-cos2a\right]\)
\(=\frac{1}{2}\left[1-2sin^2b-1+2sin^2a\right]\)
\(=sin^2a-sin^2b\)
\(=1-cos^2a-1+cos^2b=cos^2b-cos^2a\)
Câu này bạn cũng ghi đề ko đúng
\(cos\left(a+b\right)cos\left(a-b\right)=\frac{1}{2}\left[cos2a+cos2b\right]\)
\(=\frac{1}{2}\left[2cos^2a-1+1-2sin^2b\right]=cos^2a-sin^2b\)
\(=1-sin^2a-1+cos^2b=cos^2b-sin^2a\)


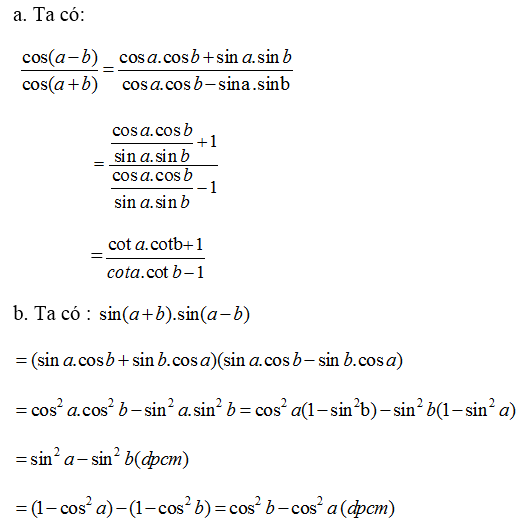
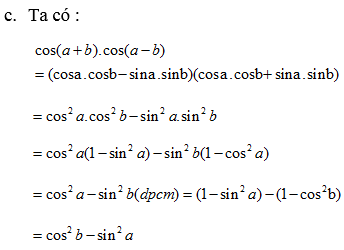
A = 2(1 - sin2α)2 - sin4α + sin2α (1-sin2α) + 3sin2α
=2 - 4sin2α + 2sin4α - sin4α + sin2α - sin4α + 3sin2α
= 2
\(A=2\cos^4\alpha-\sin^4\alpha+\sin^2\alpha.\cos^2\alpha+3\sin^4\alpha+3\cos^2\alpha.\sin^2\alpha\)
\(A=2\sin^4\alpha+2\cos^4\alpha+4\sin^2\alpha.\cos^2\alpha\)
\(A=2\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-2\sin^2\alpha.\cos^2\alpha\right]+4\cos^2\alpha\sin^2\alpha=2\)