Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Đồ thị được vẽ như hình bên.
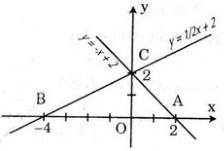
b) Giao của đường thẳng y = -x + 2 với Ox là B(2; 0).
Vì hai đường thẳng y = 0,5x + 2 và y = -x + 2 đều có tung độ gốc là 2 nên giao của chúng là C(0; 2).
Ta có tg A = 0,5. Suy ra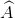 
≈ 26034’.
Vì ∆BOC là tam giác vuông cân nên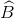 
=450 .
Suy ra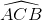 
≈ 1800 – (26034’ + 450) = 108026’.
c) Ta có AB = 6 (cm), AC =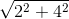 
= 2√5 (cm), BC = 2√2 (cm).
Do đó chu vi của ∆ABC là 6 + 2√5 + 2√2 (cm).
Diện tích của ∆ABC là: 
AB . OC = . 6 . 2 = 6 (cm2).
Bài giải:
a) Đồ thị được vẽ như hình bên.
b) Giao của đường thẳng y = -x + 2 với Ox là B(2; 0).
Vì hai đường thẳng y = 0,5x + 2 và y = -x + 2 đều có tung độ gốc là 2 nên giao của chúng là C(0; 2).
Ta có tg A = 0,5. Suy ra 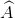≈ 26034’.
Vì ∆BOC là tam giác vuông cân nên 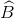=450 .
Suy ra 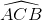≈ 1800 – (26034’ + 450) = 108026’.
c) Ta có AB = 6 (cm), AC = 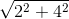= 2√5 (cm), BC = 2√2 (cm).
Do đó chu vi của ∆ABC là 6 + 2√5 + 2√2 (cm).
Diện tích của ∆ABC là: AB . OC = . 6 . 2 = 6 (cm2).
a) (d1): y = (m+2)x - m + 1 có hệ số a1 = m+2, b1 = -m +1
(d2): y = (2m-5)x + m có hệ số a2 = 2m - 5, b2 = m
Vậy khi m = 7 thì (d1) song song với (d2)
Bài 2: Cho đường thẳng (AB): y = -1/3x + 2/3; (BC): y = 5x+1; (CA): y = 3x. Xác định tọa độ ba đỉnh của tam giác ABC
Hướng dẫn giải
Điểm B là giao điểm của (AB) và (BC):
Phương trình hoành độ giao điểm B:
Điểm A là giao điểm của (AB) và (AC) nên:
Phương trình hoành độ giao điểm A:
-1/3x + 2/3 = 3x
⇔ 3x + 1/3x = 2/3
⇔ x.10/3 = 2/3
⇔ x = 1/5
=> y = 3.1/5 = 3/5
Vậy A(1/5;3/5)
Điểm C là giao điểm của (BC) và (AC) nên:
Phương trình hoành độ giao điểm C:
5x + 1 = 3x
⇔ 2x = -1
⇔ x = -1/2
> y = 3.(-1/2) = -3/2
Vậy C(-1/2;-3/2)
Bài giải:
a) Xem hình bên
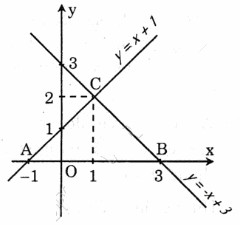
b) A(-1; 0), B(3; 0), C(1; 2).
c) Chu vi ∆ABC bằng 4(1 + √2).
Diện tích ∆ABC bằng 4cm2 .
\(T=x^4+y^4+z^4\)
áp dụng bđt bunhia cốp -xki với bộ số \(\left(x^2,y^2,z^2\right);\left(1,1,1\right)\)
\(\left(\left[x^2\right]^2+\left[y^2\right]^2+\left[z^2\right]^2\right)\left(1^2+1^2+1^2\right)\ge\left(x^2+y^2+z^2\right)^2\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(2xy+2yz+2xz\right)^2}{3}\)(bđt tương đương)
\(\left(x^4+y^4+z^4\right)\ge\frac{4}{3}\)
dấu "=" xảy rakhi và chỉ khi
\(\hept{\begin{cases}\frac{x^2}{1}=\frac{y^2}{1}=\frac{z^2}{1}\\x=y=z=1\end{cases}< =>\frac{1^2}{1}=\frac{1^2}{1}=\frac{1^2}{1}}\)(luôn đúng)
vậy dấu "=" có xảy ra
\(< =>MIN:T=\frac{4}{3}\)
sửa dòng 3 dưới lên
\(T\ge\frac{\left(xy+yz+xz\right)^2}{3}=\frac{1}{3}\)
Dấu ''='' xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)
Vậy GTNN T là 1/3 khi \(x=y=z=\frac{\sqrt{3}}{3}\)