Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi 2 số cần tìm là a và b ( \(a,b\inℕ^∗\))
Theo bài, ta có: \(\frac{a}{b}=\frac{4}{7}\)\(\Rightarrow\frac{a}{4}=\frac{b}{7}\)
Đặt \(\frac{a}{4}=\frac{b}{7}=k\left(k\inℕ^∗\right)\)\(\Rightarrow a=4k\); \(b=7k\)
Nếu lấy số thứ nhất chia cho 4, số thứ 2 chia cho 5 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị
\(\Rightarrow\)Ta có phương trình : \(\frac{7k}{5}-\frac{4k}{4}=2\)
\(\Leftrightarrow\frac{7k}{5}-k=2\)\(\Leftrightarrow\frac{7k}{5}-\frac{5k}{5}=\frac{10}{2}\)
\(\Leftrightarrow7k-5k=10\)\(\Leftrightarrow2k=10\)\(\Leftrightarrow k=5\)( thoả mãn ĐK )
\(\Rightarrow a=5.4=20\)và \(b=5.7=35\)
Vậy số bé là 20 và số lớn là 35
Gọi M là điểm chia đoạn AB (AM > MB) và AB có độ dài bằng a.
Gọi tỉ số cần tìm là x (x > 0).
Theo đề bài: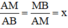 
⇒ AM = x.AB = ax;
⇒ M B = x . A M = x . a x = a x 2
Ta có: MA + MB = AB
⇒ a x + a x 2 = a ⇔ x 2 + x = 1 ⇔ x 2 + x − 1 = 0
Có a = 1 ; b = 1 ; c = -1 ⇒ Δ = 1 – 4.1.(-1) = 5 > 0.
Phương trình có hai nghiệm
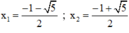
Chỉ có nghiệm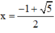 
thỏa mãn điều kiện.
Vậy tỉ số cần tìm là: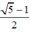 
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.
Gọi M là điểm chia đoạn AB (AM > MB) và AB có độ dài bằng a.
Gọi tỉ số cần tìm là x (x > 0).
Theo đề bài: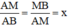 
⇒ AM = x.AB = ax;
⇒MB = x.AM = x.ax = ax2
Ta có: MA + MB = AB
⇒ ax + ax2 = a
⇔ x2 + x = 1
⇔ x2 + x – 1 = 0.
Có a = 1 ; b = 1 ; c = -1 ⇒ Δ = 1 – 4.1.(-1) = 5 > 0.
Phương trình có hai nghiệm
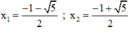
Chỉ có nghiệm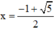 
thỏa mãn điều kiện.
Vậy tỉ số cần tìm là: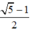 
Vì AP//DN nên theo định lí Ta-lét ta có
\(\frac{CN}{BK}=\frac{CQ}{QK}=\frac{CD}{KP}\)
\(\Rightarrow CN.KP=CD.BK\)
Câu trả lời là không. Và lời giải khá đơn giản. Thay dấu cộng bằng số 1 và dấu trừ bằng - 1. Xét tích tất cả các số trên bảng vuông. Khi đó, qua mỗi phép biến đổi, tích này không thay đổi (vì sẽ đổi dấu 4 số). Vì vậy, cho dù ta thực hiện bao nhiêu lần, từ bảng vuông (1, 15) sẽ chỉ đưa về các bảng vuông có số lẻ dấu -, có nghĩa là không thể đưa về bảng có toàn dấu cộng.
Bạn tham khảo nha
Hai tam giác được gọi là đồng dạng nếu một trong chúng bằng với một tam giác nhận được từ tam giác kia sau một phép vị tự. Các điều kiện cần và đủ để hai tam giác đồng dạng:
- Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng.
- Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng.
- Hai tam giác có hai cặp cạnh tương ứng tỷ lệ, góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng.