Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)

Bạn tự vẽ hình nhé.
Qua A ta kẻ đường thẳng D song song với BC tạo ra 3 góc tại điểm A lần lượt là góc A1 ; góc A2 ; và góc A3
Vì BC song song với đường thẳng D nên :
+ ) CBA = A1 ( so le trong )
+ ) BCA = A1 ( so le trong )
=> BAC + BCA + ABC = A1 + A2 + A3
Hiển nhiên A1 + A2 + A3 = 180o vì tổng 3 góc là góc bẹt.
=> Tổng 3 góc trong tam giác là 1800
k nha mọi người !!k nha moi nguoi !!
tự vẽ hình nhé:
Qua A vẽ đường thẳng d song song BC tạo ra 3 góc tại điểm A lần lượt là góc A1 ; A2 ; A3
vì d // BC (cách vẽ)
=> góc CBA = góc A1 (so le trong)
góc BCA = góc A3 (so le trong)
=> góc BAC + góc BCA + góc ABC = 1800
vì vậy góc A1 + góc A2 + góc A3 = 1800 vì tổng 3 góc là góc bẹt
=> tổng 3 góc trong tam giác là 1800
ok mk nha1! 56456457675687684575675678578768769762353463466456456576575756753

Đa giác có tổng số đo các gióc bằng 1 nửa tổng số đo các góc ngoài
a, Tam giác
b, Tứ giác
c, ngũ giác
d lục giác
đáp á là: b, Tứ giác

Bởi vì nếu vẽ bất cứ một đường chéo nào trên tứ giác thì đều chia tứ giác thành hai tam giác. Mà tổng các góc trong 1 tam giác bằng 180 độ suy ra tổng các góc trong 1 tứ giác bằng 180. 2=360 độ

Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4.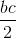 (1)
(1)
SGHIK= (b+c)2 = Sa + 4.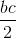 (2)
(2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa
