Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
S A B x x x x 20 cm
Mình vẽ hơi xấu nên nó k bằng nhau ^_^
a) ta thấy chiều dài của hcn B là cạnh của đáy S
Cạnh đầu tiên của đáy là 20 - 2x
Ta thấy chiều dài của hcn A là cạnh của đáy S
Cạnh thứ hai của đáy là 20 - 2x
Vậy Diện tích đáy S là (20 - 2x)2
b) khi gấp lại thành hình hộp chữ nhật thì x cũng là chiều cao của hình nên
Thể tích HHCN là x(20 - 2x)2
a)Xét tam giác BDC và tam giác HBC có :
\(\widehat{DBC}=\widehat{BHC}\left(=90^o\right)\)
Chung \(\widehat{BCD}\)
\(\Rightarrow\) Tam giác BDC đồng dạng với tam giác HBC ( g-g )
b) Do tam giác BDC đồng dạng với tam giác HBC
\(\Rightarrow\frac{DC}{BC}=\frac{BC}{HC}\)
\(\Leftrightarrow\frac{25}{15}=\frac{15}{HC}\)
\(\Leftrightarrow HC=9\left(cm\right)\)
Ta có : \(HD+HC=DC\)
\(\Leftrightarrow HD+9=25\)
\(\Leftrightarrow HD=16\left(cm\right)\)
Gọi x ( ngàn đồng ) là giá niêm yết của bàn ủi ( 850>x>0)
=> giá niêm yết của quạt điện là : 850 - x (ngàn đồng)
Giá bán thực tế của bàn ủi là: x-(x.10%) <=>x - \(\frac{x}{10}\)(ngàn đồng)
=> giá bán thực tế của quạt điện là (850-x).20% <=>850 -\(\frac{850-x}{5}\)(ngàn đồng)
Do anh Bình đã trả ít hơn 125 ngàn đồng khi mua giá thực tế nên ta có pt:
\(x-\frac{x}{10}+\left(850-x\right)-\frac{850-x}{5}=725\)
<=> \(\frac{10x}{10}-\frac{x}{10}+\frac{8500-10x}{10}-\frac{2\left(850-x\right)}{10}=\frac{7250}{10}\)
=> 10x - x + 8500 - 10x -1700 + 2x = 7250
<=> x = 450(tm)
Vậy chênh lệch giữa giá bán thực tế và giá bán niêm yết của bàn ủi là: 450.10%= 45 ngàn đồng
..........................................................................................quạt điện là : 400. 20% = 80 ngàn đồng
\(\frac{\sqrt{6}+5\sqrt{2}}{\sqrt{2}}-\frac{2}{\sqrt{3}-1}\)
\(\Leftrightarrow\frac{\left(\sqrt{3}-1\right)\left(\sqrt{6}+5\sqrt{2}\right)}{\sqrt{2}\left(\sqrt{3}-1\right)}-\frac{2\sqrt{2}}{\sqrt{2}\left(\sqrt{3}-1\right)}\)
\(\Leftrightarrow\frac{3\sqrt{2}+5\sqrt{6}-\sqrt{6}-5\sqrt{2}-2\sqrt{2}}{\sqrt{2}\left(\sqrt{3}-1\right)}\)
\(\Leftrightarrow\frac{-4\sqrt{2}+4\sqrt{6}}{\sqrt{6}-\sqrt{2}}\)
\(\Leftrightarrow\frac{4\left(\sqrt{6}-\sqrt{2}\right)}{\sqrt{6}-\sqrt{2}}\)
\(\Leftrightarrow4\)
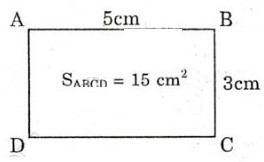
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
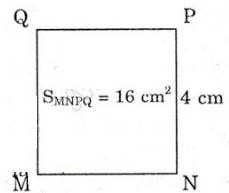
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có 
≥ √ab
Suy ra ab ≤ .
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh .
Trên hình a= 5cm, b = 3cm, = 4cm
a - = 1cm, - b = 1cm
Do đó
SEBCG = b. ( a- ) = 3.1 = 3 (cm2).
SDGHI = . ( - b ) = 4.1 = 4 (cm2).
SAEGD = b. = 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a - , cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng - b, cạnh kia bằng .
Mà a - bằng - b và b < ( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
Hướng dẫn giải:
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có ≥ √ab
Suy ra ab ≤ .
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh .
Trên hình a= 5cm, b = 3cm, = 4cm
a - = 1cm, - b = 1cm
Do đó
SEBCG = b. ( a- ) = 3.1 = 3 (cm2).
SDGHI = . ( - b ) = 4.1 = 4 (cm2).
SAEGD = b. = 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a - , cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng - b, cạnh kia bằng .
Mà a - bằng - b và b < ( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
