Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
) vẽ hình giùm mình lun nha
làm được bài nào thì làm hộ mìn vs nha
giúp mình bài 2 nha
\(B=\frac{1}{x^4}+\frac{1}{y^4}=\frac{y^4}{x^4.y^4}+\frac{x^4}{x^4.y^4}=\frac{x^4+y^4}{x^4y^4}=\frac{\left(x^2+y^2\right)^2-2x^2y^2}{x^4y^4}=\frac{\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2}{x^4y^4}\)
\(=\frac{\left[20^2-2.\left(-44\right)\right]^2-2.\left(-44\right)^2}{\left(-44\right)^4}=\frac{488^2+3872}{3748096}=\frac{234272}{3748096}=\frac{7321}{117128}\)
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
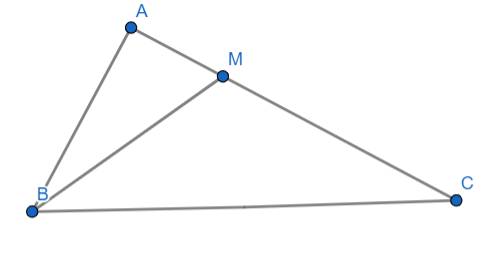
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)
a) Xét hai tam giác ABE và ACD có:
\(\widehat{ACD}=\widehat{ABE}\left(gt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACD\left(g.g\right)\)
b) Ta có: \(\Delta ABE\sim\Delta ACD\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
bạn vẽ đẹp wá
có ảnh nào nữa không ?????
cho mk xem
trời ơi đúng là 1 kiệt tác
đệp wá bn ơi