Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
Ta có
\(BC\perp AB';B'C'\perp AB'\) => BC//B'C'
\(\Rightarrow\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\Rightarrow\dfrac{x}{x+h}=\dfrac{a}{a'}\)
\(\Rightarrow a'x=ax+ah\Rightarrow x\left(a'-a\right)=ah\Rightarrow x=\dfrac{ah}{a'-a}\left(dpcm\right)\)
Xét tam giác ABCABC có BC⊥ AB′BC⊥ AB′ và B′C′⊥AB′B′C′⊥AB′ nên suy ra BCBC // B′C′B′C′.
Theo hệ quả định lí Thalès, ta có: ABAB′ =BCBC′AB′AB =BC′BC
Suy ra xx+h =aa′x+hx =a′a
a′.x=a(x+h)a′.x=a(x+h)
a′.x−ax=aha′.x−ax=ah
x(a′−a)=ahx(a′−a)=ah
x=aha′ −ax=a′ −aah.
.png)
\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)
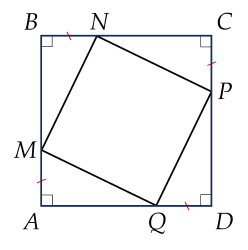
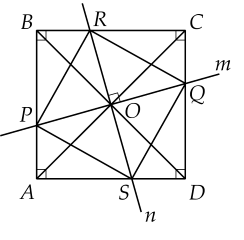
a) Do ABCD là hình vuôn nên:
\(AB=BC=CD=AD\)
Mà: \(\left\{{}\begin{matrix}AB=AM+MB\\BC=BN+NC\\CD=CP+PD\\AD=DQ+QA\end{matrix}\right.\)
Lại có: \(AM=BN=CP=DQ\)
\(\Rightarrow MB=NC=PD=QA\left(dpcm\right)\)
b) Xét \(\Delta QAM\) và \(\Delta NCP\) có:
\(\widehat{A}=\widehat{C}=90^o\left(gt\right)\)
\(AM=CP\left(gt\right)\)
\(QA=NC\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP\left(c.g.c\right)\)
c) Xét các tam giác: \(\Delta QAM,\Delta NCP,\Delta PDQ,\Delta MBN\) ta có:
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\left(gt\right)\)
\(AM=BN=CP=DQ\left(gt\right)\)
\(MB=NC=PD=QA\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP=\Delta PDQ=\Delta MBN\left(c.g.c\right)\)
\(\Rightarrow MQ=QP=PN=NM\) (các cạnh tương ứng)
\(\Rightarrow MNPQ\) là hình thoi (1)
Xét tam giác QAM ta có:
\(\widehat{QMA}+\widehat{AQM}=180^o-90^o=90^o\)
Mà: \(\Delta QAM=\Delta MBN\left(cmt\right)\)
\(\Rightarrow\widehat{BMN}=\widehat{AQM}\) (hai góc tương ứng)
\(\Rightarrow\widehat{BMN}+\widehat{QMA}=90^o\)
Lại có: \(\widehat{BMN}+\widehat{QMA}+\widehat{NMQ}=180^o\)
\(\Rightarrow\widehat{NMQ}=180^o-90^o=90^o\) (2)
Từ (1) và (2) ta có MNPQ là hình vuông
a) ����ABCD là hình vuông nên ��=��=��=��AB=BC=CD=DA
Mà ��=��=��=��AM=BN=CP=DQ.
Trừ theo vế ta được ��−��=��−��=��−��=��−��AB−AM=BC−BN=CD−CP=DA−DQ
Suy ra ��=��=��=��MB=NC=PD=QA
Xét tam giác QAM và tam giác NPC có:
góc A = góc C = 90 độ
AQ=NC(cmt)
AM=CP(gt)
=>Tam giác QAM= tam giác NPC(c.g.c)
c)=> NP = MQ ( hai cạnh tương ứng)
Chứng minh tương tự như phần b ta có: Tam giác QAM= tam giác PDQ và tam giác QAM= tam giác MBN
Khi đó: MQ=PQ, MN=MQ và góc AMQ= góc DQP
Mà góc AMQ+AQM=90 độ
=>góc DQP+ góc AQM= 90 độ
Do đó góc MQP = 90 độ
tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi
Lại có góc MQP = 90 độ nên là hình vuông
Vậy tứ giác MNPQ là hình vuông
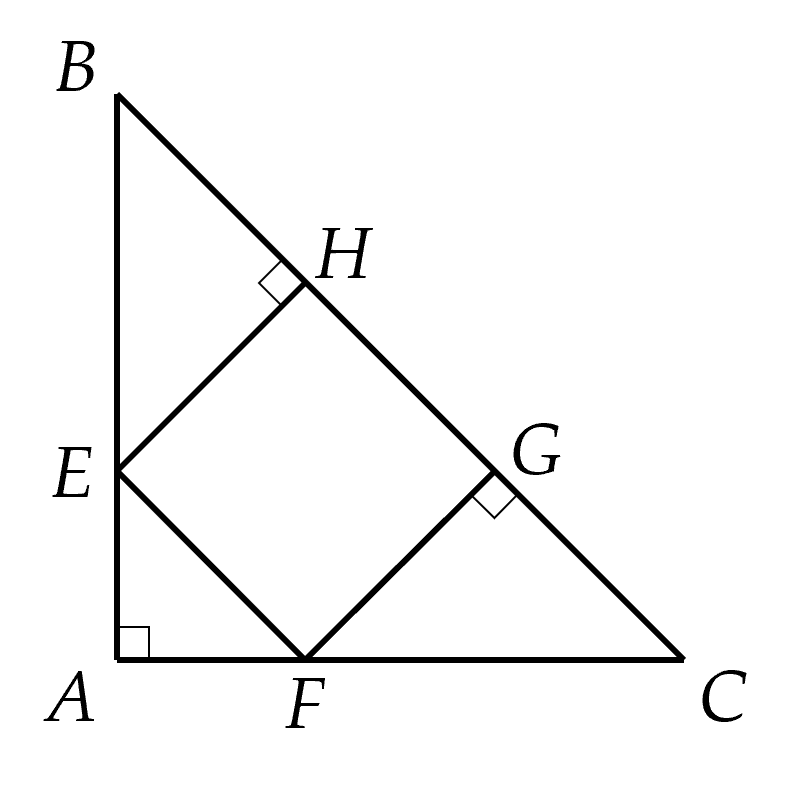
a) Δ��� Tam giác ABC vuông cân nên góc B= góc C = 45 độ
Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ
Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ
Vậy tam giác BEH vuông tại H
b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE
Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)
Tứ giác EFGH có EH//FG, EH=FG
=>tứ giác EFGH là hình bình hành
Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật
Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông
Vậy EFGH là hình vuông
a) Δ���ΔABC vuông cân nên �^=�^=45∘.B=C=45∘.
Δ���ΔBHE vuông tại �H có ���^+�^=90∘BEH+B=90∘
Suy ra ���^=90∘−45∘=45∘BEH=90∘−45∘=45∘ nên �^=���^=45∘B=BEH=45∘.
Vậy Δ���ΔBEH vuông cân tại �.H.
b) Chứng minh tương tự câu a ta được Δ���ΔCFG vuông cân tại �G nên ��=��GF=GC và ��=��HB=HE
Mặt khác ��=��=��BH=HG=GC suy ra ��=��=��EH=HG=GF và ��EH // ��FG (cùng vuông góc với ��)BC)
Tứ giác ����EFGH có ��EH // ��,��=��FG,EH=FG nên là hình bình hành.
Hình bình hành ����EFGH có một góc vuông �^H nên là hình chữ nhật
Hình chữ nhật ����EFGH có hai cạnh kề bằng nhau ��=��EH=HG nên là hình vuông.
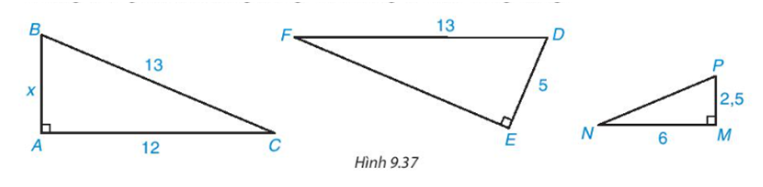
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
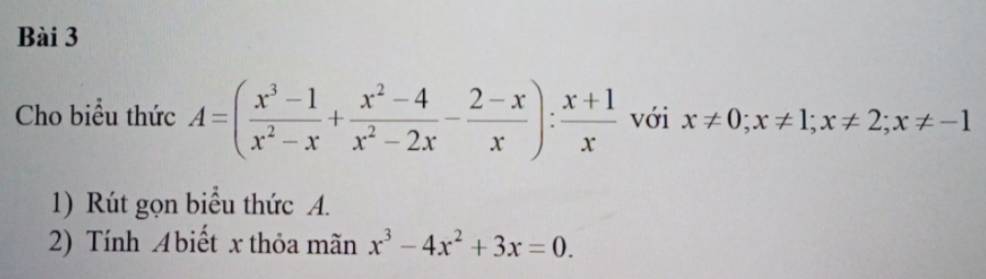
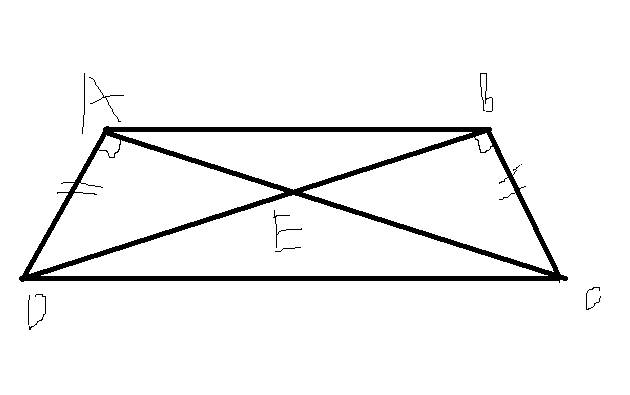
a: Xét ΔADC vuông tại A và ΔBCD vuông tại B có
AD=BC
DC chung
=>ΔADC=ΔBCD
b: ΔADC=ΔBCD
=>góc ACD=góc BDC
=>góc EDC=góc ECD
=>ΔEDC cân tại E
c: Xét ΔEAD vuông tại A và ΔEBC vuông tại B có
ED=EC
AD=BC
=>ΔEAD=ΔEBC
=>EA=EB
Xét ΔEAB và ΔECD có
EA/EC=EB/ED
góc AEB=góc CED
=>ΔEAB đồng dạng với ΔECD
=>góc EAB=góc ECD
=>AB//CD