Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

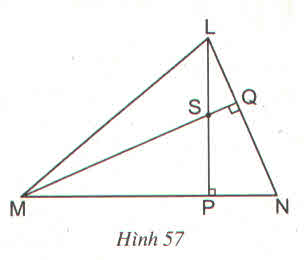
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)

+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :
ΔNMQ vuông tại Q có:


a) Ta có:
OA _|_ OM (gt)
=> AOM = 90 độ
Tương tự ta có:
BON = 90 độ
b) Ta có:
BOM + MON = 90 độ
AON + MON = 90 độ
=> BOM = AON

Vì \(OA\perp OM\)( gt )
\(\Rightarrow\)\(\widehat{AOM}=90\)độ
Tương tự : \(\widehat{BON}=90\)độ
b) Vì :
\(\widehat{BOM}+\widehat{MON}=90\)độ
\(\widehat{AON}+\widehat{MON}=90\)độ
\(\Rightarrow\)\(\widehat{BOM}=\widehat{AON}\)
hay \(\widehat{NOA}=\widehat{MOB}\)

a) "Chìa khóa" ở hai tam giác vuông HEB và HDC đó, có 2 góc đối đỉnh, Tổng 2 góc nhọn là 90o
b) Tính A^ . Rồi tính HCD^ và ABD^ . Dựa vào 2 số đo vừa tìm được và số đo ở đề bài tính HBC^ và HCB^ .
Một tam giác, có được số đo độ 2 góc rồi thì góc còn lại làm sao nhỉ ^^?! Trình bày ngắn gọn, có điều kiện CẦN và ĐỦ nhé ^^!
NS lak gì?
LM lak gì?
Thiếu đề rồi bạn ơi
Thiếu đề rồi bạn ơi